- Return Exam I.
- Multiply your score by 1.5: that's your curved score.
- Now: If you'll redo your exam (here's a link to it), I'll average your current
score with your score on the redo. That average will be
treated as your final percentage.
Your "redo" should be very neat and tidy. You may work with with others, but your final work, on your own test, should be your own.
These are due Thursday of next week. Hand them in attached with your original exam.
But we do need to take care of some serious errors....
- Your homework for section 11.2 is due next time, 10/8.
- Here's how we make sense of an infinite sum:
- From the sequence
we define a new sequence
:
These are called partial sums. If
Then we say that
exists, and is equal to L. More formally,

Now geometric series are sufficiently important that it's useful to include that special case:

There's a really fun proof of the first part above, based on a trick. Let's have a look at it.

This theorem tells us that if the terms of a sequence aren't asymptotic to the x-axis, we can forget about the partial sums converging.
Finally, series behave the way we'd hope (provided they're convergent):

- Examples:
- #7, p. 554
- #8, p. 554 (compare to Taylor series error bound)
- #33, p. 554
- Reflect on #36, p. 555. Recursive actions and definitions give rise to these types of geometric sums.
- Along the same lines: #45, p. 555
- #52, p. 556
- Beautiful spiral "proofs" of some infinite series
- From the sequence
- concerns several different means of testing for convergence of
series with all positive terms (obviously, if we're dealing with series
of all negative terms, similar results are going to apply).
- We're not so concerned with the actual limits (that is the values
of the series) as we are with the convergence (or divergence) of the
series.
- Theorems:

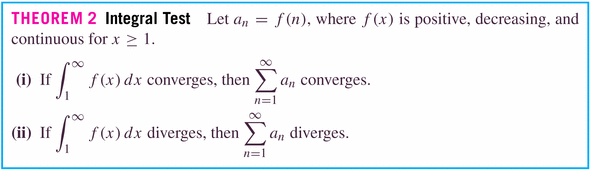
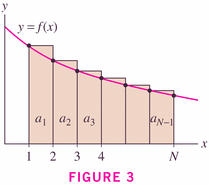
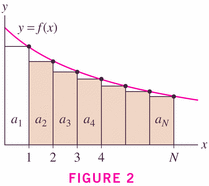
Theorem 3 is just a corollary of Theorem 2, where the integrals are the obvious power functions:

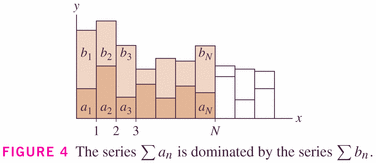
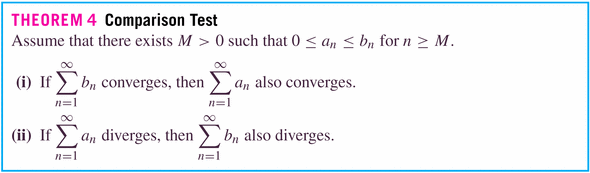

This theorem says that, in the long run, one series has terms which are simply a constant times the terms in the other series.
- Examples:
- Integral Test: #9, 10, p. 563
- Comparison Test: #20, p. 563
- Limit Comparison Test: #34, p. 563
- Divergence of the harmonic series (and dominoes!)