Day 10 in Mat129

Today:

• Announcements
  • Hand in the problem set pp. 73, #77, 78, 79
  • New assignment:

    Tue

    2/2

    Section 3.1/3.2

    Read 3.3 Begin on-line homework assignments 3.1 and 3.2 (due Monday, 2/8)

• Roll

• Section 3.1: The Definition of the Derivative
  • "time, position, velocity"
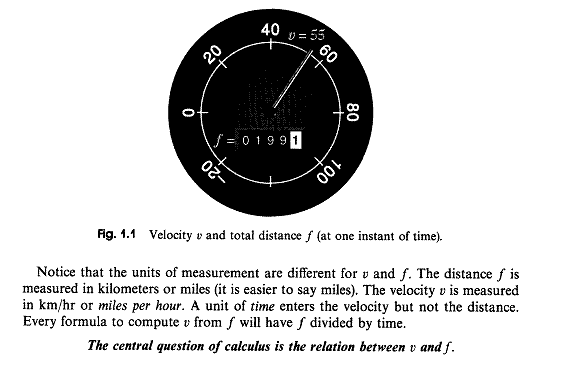
    • If we have the record of the position, could we recover the velocity?
    • If we have the record of the velocity, could we recover the position?

  • Secant lines approximating tangent lines....

  • The definition:

  • Example problems:
    • #5, p. 103 (including tangent lines)
    • #21, p. 104 (including tangent lines)
    • #26, p. 104 (including tangent lines)
    • #40, p. 105 (including tangent lines)
    • #49, p. 105 (approximating derivatives with average rates of change)
    • How would you model the rates of change of Wind power?

• Section 3.2: The Derivative Function
  • The definition

  • Here's an example of an important function:
    

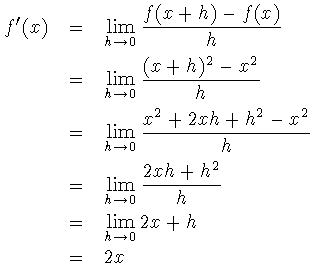
  • A little trickier one: #6, p. 116

  • Derivatives of constant functions and the function f(x)=x

  • Rules that help us avoid the definition! (with Proofs)

    • The sum rule

      works as we'd hope: the derivative of a sum is the sum of the derivatives

    • The constant multiple rule (makes sense)

    • The power rule (via dominoes -- i.e., mathematical induction)

    • NOTE: at this point we have all the rules necessary to differentiate all polynomials, without needing to resort to the definition!

  • #63 and 64, p. 118

  • Note Theorem 3 (p. 113): differentiability implies continuity (we know that already!)

  • But continuity does not imply differentiability -- examples?

• Section 3.3

  • The product rule

    Rats! "The derivative of the product is not the product of the derivatives."

  • The quotient rule (Rats again!)

• Javamath