Day 04, MAT115

• A natural number that can be divided evenly (that is, without remainder) by only two distinct natural numbers: 1 and itself.
• NOTE: when mathematicians say "distinct" natural numbers, they mean that they need to be different; and so the number 1 is not prime.
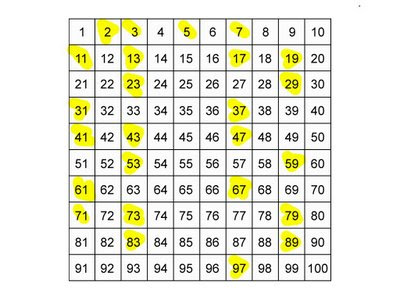
• We can find the primes using the Sieve of Eratosthenes (here's an animation)
• I didn't get to tell you an interesting story about Eratosthenes and his measurement of the Earth's circumference last time....

• Every natural number greater than 1 is either prime, or it can be expressed as a product of prime numbers (in one and only one way -- order of the product aside).

• Examples:
  • 42=2*21=2*3*7
  • 8=2*2*2 (prime factors can repeat)
  • 1729 = 7*247 = 7*13*19
  • It's often good to illustrate this process using a tree. Trees again! They're very useful....
  • If you can't factor a number by any prime less than or equal to the number's square root, then the number is prime. Why is this?
  • 127: its square root is approximately 11.27. We don't need to go past 11 to find its factors.
  • The general procedure (and one that we'll see repeated time and again in mathematics):
    do it once, then do it again, and again, and again.... until done (or tired).

    I'll call this out often, saying simply "do it again...." I mean that you can apply exactly the same procedure just used, often on a simpler problem.

  • Upshot: We can "decompose" (or factor) natural numbers using prime numbers and products, in a unique way.

  • Notice that if we allowed 1 to be prime, then the decomposition wouldn't be unique. For example, 6=3*2=3*2*1 -- so there wouldn't be a unique way of writing 6 (up to interchanging the order in the product, i.e. 6=2*3).

• Euclid - he of geometry fame -- concluded that there are infinitely many prime numbers.

So here's a question we'll come back to:

if there are infinitely many natural numbers, and there are infinitely many primes, are there more natural numbers than primes, since every prime is a natural number but not every natural number is a prime?

• Twin primes conjecture -- To this day no one knows if there are an infinite number of primes p and p+2. For example 17 and 19, or 29 and 31, are "twin primes"

• Goldbach conjecture - Every even number (greater than two) is the sum of exactly two prime numbers. For example 18=11+7
• Primes of the form 4k+1 can be written as the sum of two squares in exactly one way: so for k=3,

• Primes of the form 4k-1 can never be written as the sum of two squares. So for k=3, 11=what?? Try the few possibilities.

• In particular, rational numbers are ratios of whole numbers (natural numbers): where m and n are integers (i.e. natural numbers, perhaps with a negative sign).

• Let's go through that decimal conversion in our text:
  

  The process of "long division" is another example of a "do it again" phenomenon.

• Let's try another:
  

  Rational numbers always have either terminating or repeating decimal representations. Irrational numbers don't repeat, or terminate. is an example.

• Multiplying fractions is carried out by multiplying numerators by numerators, denominators by denominators. One place we often see these kinds of problems is in retail clothing. For example, you're at Kohl's, and they have the 70%-90% off rack. Here's how they might arrive at that for a given item: you take half off another price, already reduced.

  That is, if we take half off an item that's already had half off, what do we get? The price is

  of its original cost (25% of original cost -- so it's 75% off).

  If you take half off three times, some people think that they'll be paid half the item's value to take it away. Hah!;) What are you really paying of the original price?

• Adding fractions is really the bane of students. For this, we need a common denominator. The rule is actually pretty simple:
  

  So if you eat of the pie, and then of the pie, you've eaten a total of

  

  of the pie. It's that easy!

  These types of fractions (with numerators of 1) are especially important in Egyptian division (which we'll study next week).

  Let's do that Egyptian fraction example on p. 15. It's a "do it again" situation:

  

Is it possible to reach one wall from the opposing wall? Zeno argued that no, it's not possible.

In the process of discussing this we'll add together an infinite number of fractions (there's a nightmare for you!):