- Your assignment over 6.4 is due today
- Tonight is the first STEM pizza party (pizza at 6:00, UC135). Tutoring afterwards.
- I've reserved computer lab 310 for Friday, 9/12, at 9:00. So next week those who are able may join me as we go over some of the basics of Mathematica. I've also reserved it for a couple of more Fridays, the 26th of September and the 33rd of September (figure it out!:).
- The first place to start is the geometric perspective, perhaps.
As usual, we're focused on the undoing property: if the question for us begins as "What is sine of 30 degrees?", the undoing question is "Whose sine is
?"
We should immediately observe that the original question has a unique solution, whereas the "undoing question" does not. Because sine is not one-to-one, we shouldn't be surprised. But this is an issue: how do we create a useful "inverse" of a non-invertible function?
- Well, we need to worry in particular about three cases: sine,
cosine, and tangent (the others -- secant, etc. -- I don't really worry
about too much, but they do sometimes come into play):
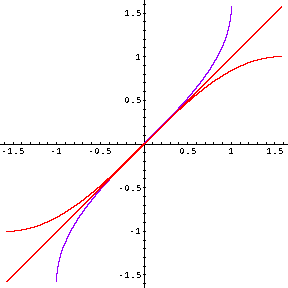
- Two of these inverse functions are shown in their entirety; the other isn't. Which is which?
- What features of a graph would have helped us to identify these more easily?
- One of these also illustrates the fact that a function can increase forever, without tending to infinity -- it asymptotes to a finite value. What is it?
- The graphical definitions of these functions are easy, carried out
via the mirror. But what are the properties of these inverses?
For example, what are their derivatives? These we've carried out before, using the amazing rule for inverse functions -- do you remember it?
Let's try it with arctan...
- Can you relate arcsin and arccos? Can you obtain one from the
other using shifts, reflections, etc.?
- Let's look at a few problems involving these curious inverse
functions:
- 14 (a test of your trig identities and the relationship of trig functions to triangles)
- 22
- 63
- 48
- This topic is considered supplementary by the department, but I
like to include it. The graph of one of these functions is one you've
been seeing all of your life, but you probably don't have a name for it
(yet): the catenary (or "hanging chain").



- Here are the graphs of the two functions
and
:
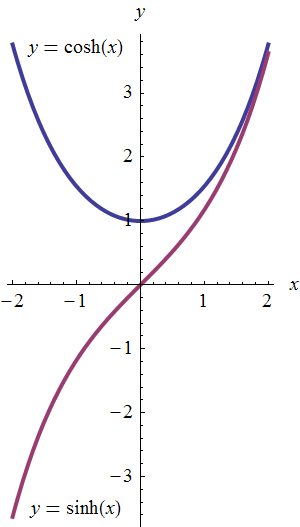
which have formulas
and
- Let's derive their inverses, and the derivatives of these
"Hyperbolic functions" and their inverses.
- Then we'll do some problems:
- #21, p. 467
- #48
- #49
- Catenaries and parabolas are closely related: a suspension bridge cable starts as a catenary, but under load its shape takes the form of a parabola!
- In financial mathematics we tend to use an unusual base for an
exponential:
- You may have encountered a few laws such as The rule of 72 (70, 71,
69.3,...) to calculate doubling time: forget them! Just do the
math: the question is
For what value of t is ?
Solving for t in
, we get
where n is the number of compoundings per year, and r is given as a decimal (e.g. 9% is represented by .09). This is the doubling time.
When compounding is continuous (i.e.
), this reduces to the very lovely rule
- Now, how do we know that
?
?
The answer, of course, is L'Hopital's Rule, which is useful in solving certain indeterminate limits:

Let's rewrite it a little: we want to show that
- Here's the general situation:

- And if the limit of the quotient of the derivatives is
indeterminate, then iterate -- that is, do it again! Then work with the
ratio of the second (or higher) derivatives.
- Motivation of L'Hopital's Rule (requires the limit definition
of the derivative -- p. 471)
- Examples:
- Demonstration that
where
)
- Let's do a bunch of odds, #7-33, p. 477
- #70, p. 478
- #86, p. 478
- #93, p. 479
- Demonstration that