Day 12 in MAT229

Last time

Next time

Today:

Announcements:
- Your assignment over 6.4 is returned -- graded 20, 24, and 76.
  - #20: use properties of logs to make your derivatives easier. Don't forget to use the chain rule.
  - #24: IMMEDIATELY replace base-2 logs with base-e logs (ln). And don't distribute unless you need to! Factor, and cancel. Simplify, simplify, simplify!
  - #76: don't be a "dx-dropper". Don't forget your constant of integration, since this is an indefinite integral.
- Did anyone go to the first STEM pizza party?
- I've reserved computer lab 310 for this Friday, 9/12, at 9:00. So those who are able may join me as we go over some of the basics of Mathematica. I've also reserved it for a couple of more Fridays, the 26th of September and the 3rd of October.
Review of section 6.7: Hyperbolic functions
- This topic is considered supplementary by the department, but I like to include it. The graph of one of these functions is one you've been seeing all of your life, but you probably don't have a name for it (yet): the catenary (or "hanging chain").
- Here are the graphs of the two functions $sinh(x)$ and $cosh(x)$ :
  
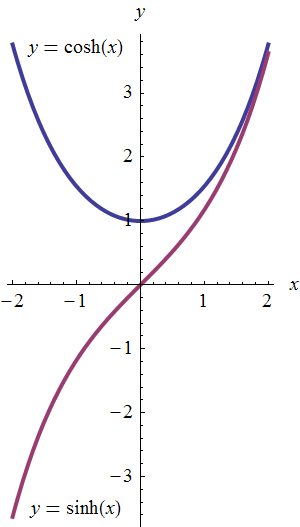
  which have formulas ${sinh(x)=\frac{{e^x-e^{-x}}}{2}}$ and ${cosh(x)=\frac{{e^x+e^{-x}}}{2}}$
- Let's derive their inverses, and the derivatives of these "Hyperbolic functions" and their inverses.
- Then we'll do some problems:
  1. #21, p. 467
  2. #48
  3. #49
- Catenaries and parabolas are closely related: a suspension bridge cable starts as a catenary, but under load its shape takes the form of a parabola!
Section 6.8: L'Hopital's Rule (Sometimes limits are kind of tricky....)
- In financial mathematics we tend to use an unusual base for an exponential:
  
  ${P(t)=P_0\left(1+\frac{r}{n}\right)^{nt}}$
- You may have encountered a few laws such as The rule of 72 (70, 71, 69.3,...) to calculate doubling time: forget them! Just do the math: the question is
  
  For what value of t is ${P(t)={P_0\left(1+\frac{r}{n}\right)^{nt}}={2{P_0}}}$ ?
  
  Solving for t in ${P_0\left(1+\frac{r}{n}\right)^{nt}=2P_0}$ , we get
  ${t=\frac{\ln 2}{n\ln(1+\frac{r}{n})}}$
  
  where n is the number of compoundings per year, and r is given as a decimal (e.g. 9% is represented by .09). This is the doubling time.
  When compounding is continuous (i.e. ${n{\to}{\infty}}$ ), this reduces to the very lovely rule
  ${\frac{\ln 2}{r}}$
- Now, how do we know that ${\lim_{n \to \infty}\frac{\ln 2}{n\ln(1+\frac{r}{n})}=\frac{{\ln{2}}}{r}}$ ? That is, how do we know that
  
  ${\lim_{n \to \infty} \ {n\ln(1+\frac{r}{n})}={r}}$ ?
  The answer, of course, is L'Hopital's Rule, which is useful in solving certain indeterminate limits:
  
  Let's rewrite it a little: we want to show that
  
  ${\lim_{n \to \infty}\frac{\ln(1+\frac{r}{n})}{{\frac{1}{n}}}={r}}$
- Here's the general situation:
- And if the limit of the quotient of the derivatives is indeterminate, then iterate -- that is, do it again! Then work with the ratio of the second (or higher) derivatives.
- Motivation of L'Hopital's Rule (requires the limit definition of the derivative -- p. 471) in the case where ${f(a)=0}$ and ${g(a)=0}$ .
  Consider ${\lim_{x\to{a}}\frac{f(x)}{g(x)}}$
- Examples:
  - Demonstration that ${\lim_{h \to 0} \frac{e^h-1}{h} = 1}$ (remember that this limit figured into the definition of $f'(x),$ where $f(x)=e^x$ )
  - Let's do 9, 11, and 15 from p. 477
  - I asked my son "What's ${0^0}$ ?" and he said "0." I tried to convince him that it should be 1 ("Any number to the 0th power is 1."). He tried to convince me that 0 to any power should be 0. His calculator said "undefined". Mathematica says "Indeterminate".
    
    What's ${\lim_{x\to{0}}{x^x}}$ ?
  - #70, p. 478
  - #86, p. 478
  - #93, p. 479

Website maintained by Andy Long. Comments appreciated.