- Have a great fall break! I hope that you get some sleep....
- Do you have a homework for me (10.3)?
- 10.1 Homework from yesterday
- Not[10.2 Homework returned:]
- 2
- 8
- 43
Let's start with a circle of radius r, centered at the origin, and see how we might adapt the "familiar formulas" to more exotic shapes:
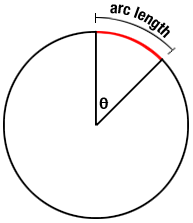
- Length: The arc length of a sector of the circle swept out
by angle
is given by
(with the familiar circumference formula being the case of sweeping out an angle of
.
So a small (infinitesimal) change
would sweep out a length of
.
- Area: The area of the sector is basically that of a half rectangle. Let's compute its dimensions.
- #1, p. 692
- 5
- 7
- #15
- 26
- 30
- 40
- 47
- 54
-
Here's our first example of a sequence:
- Definition: A sequence is a function f(n) whose
domain is a subset of the integers. The values
are called the terms of the sequence and n is called the index. For most of our sequences, the domain will be the natural numbers: {1, 2, 3, ....}.
- In the example sequence above, what do you suppose is the limit of
the sequence as
?
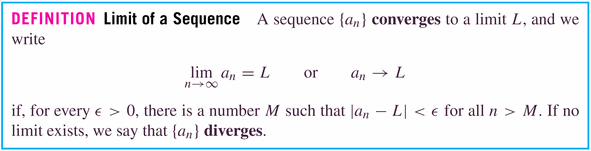
- There are lots of other sequences that we might encounter
naturally: for example, there's one in probability and statistics that
is closely related to the one we just looked at: the Poisson
distribution, which has as its probabilities the sequence
(what do you notice about the sum of the terms?).
- Other sequences might be defined in terms of a function. For
example,
where
- #3, p. 724
- #6
Other sequences are defined by "recurrence" (e.g. the Fibonacci numbers)
Example:
- #12, p. 724

Here's an especially interesting historical limit:

- One piece of good news: the obvious rules for limits are working:

Examples:
- #26, p. 724
- #27
- #29
- Some vocabulary: bounded sequences....

And some theorems related to this notion:

(especially useful for alternating sequences)

(note that the converse is false)

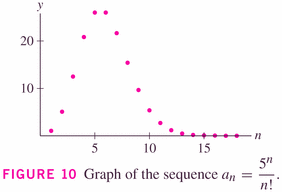
Let's use Theorem 6 to show that the sequence we initially considered is convergent:
- Geometric sequence: a sequence of the form
where r is called the common ratio.
- Examples:
- #23, p. 724
- #67
- #80

What would we get if we could add up all these (infinite!) terms? (148.4131591025766....)