- 10.1 Homework returned:
- 9 -- Here's what I'd like you to do: after trying some values of t, solve for y=f(x)=1-x^2 and realize what your curve should look like -- then fix it up! For example, the slope at (0,1) is zero....
- 28 -- some of these were tricky. One thing that a few of you commented on was boundedness -- this is really important. Some of these curves are unbounded, and others aren't. You can use that. Another thing is symmetry (surprise!). You should use that, as well. In some cases you can solve for y=f(x) for a couple. Finally you should plot the curves. You need something that will plot! As I described last time, and as Jeff knows, you can use Wolfram Alpha, even if you can't get Mathematica installed.
- 43 -- we talked about "the witch" last time. When people ask you what you're doing in calculus, tell them that you're studying witches.... (Then please begin your discussion with the limit definition of the derivative).
- You do have another homework due today, for 10.2.
Let's start with a circle of radius r, centered at the origin, and see how we might adapt the "familiar formulas" to more exotic shapes:
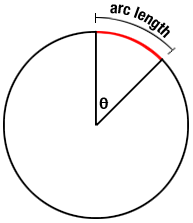
- Length: The arc length of a sector of the circle swept out
by angle
is given by
(with the familiar circumference formula being the case of sweeping out an angle of
.
So a small (infinitesimal) change
would sweep out a length of
.
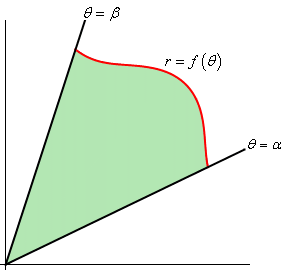
- Area: The area of the sector is basically that of a half rectangle. Let's compute its dimensions.
- #1, p. 692
- 5
- 7
- 15
- 26
- 30
- 40
- 47
- 54
-
Here's our first example of a sequence:
- Definition: A sequence is a function f(n) whose
domain is a subset of the integers. The values
are called the terms of the sequence and n is called the index. For most of our sequences, the domain will be the natural numbers: {1, 2, 3, ....}.
- In the example sequence above, what do you suppose is the limit of
the sequence as
?
- There are lots of other sequences that we might encounter
naturally: for example, there's one in probability and statistics that
is closely related to the one we just looked at: the Poisson
distribution, which has as its probabilities the sequence
(what do you notice about the sum of the terms?).
- Other sequences might be defined in terms of a function. For
example,
where
Examples:
- #3, p. 724
- #6
Other sequences are defined by "recurrence" (e.g. the Fibonacci numbers)
Example:
- #12, p. 724

Here's an especially interesting historical limit:

- One piece of good news: the obvious rules for limits are working:

Examples:
- #26, p. 724
- #27
- #29
- Some vocabulary: bounded sequences....

And some theorems related to this notion:

(especially useful for alternating sequences)

(note that the converse is false)

Let's use Theorem 6 to show that the sequence we initially considered is convergent:
- Geometric sequence: a sequence of the form
where r is called the common ratio.
- Examples:
- #23, p. 724

What would we get if we could add up all these (infinite!) terms? (148.4131591025766....)