- There's a major/minor/calculus student lunch this Friday, 11:30-1:30, upstairs by the elevators. Make sure that you stop and get something to eat. You don't even have to talk about math!
I want to start with a reminder of why we're doing all this crazy stuff about convergence/divergence.
As I've told you, it's ultimately about replacing functions with "infinite polynomials". For example, we know that the geometric series with common ratio converges if
:
We might just as well write
which converges if !
So we've replaced the rational expression by the "infinite polynomial" (for some of its domain -- but not all of it).
If x happens to be negative, then we have an alternating series on the right hand side.
-
Once again, our mission here is not necessarily the value of the
series, but may be simply knowledge of whether it converges or
not.
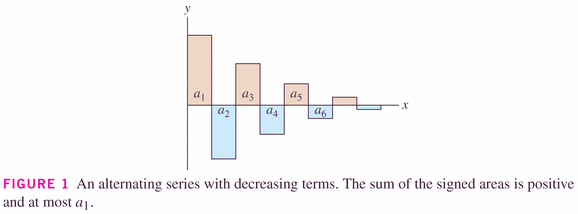
- How does the author of this image reach the conclusion that "the sum is positive and at most
"?
- How about the partial sums --
-- what are they doing?
- What are the even partial sums doing?
- What are the odd partial sums doing?
- Examples:
- The alternating harmonic series is convergent
(Example 1, p. 753).
We need to show that the terms
of the series satisfy the Leibniz test:
- the terms are positive,
- the terms are decreasing in size,
- the terms have limit of 0.
- #5, p. 755
Identify the terms
, and decide whether they satisfy the Leibniz test.
- #13
- #17
Remember that for convergence, the conditions of the test need be true only eventually: convergence is all about the tail, not the head of the sequence.
- #23
For this one, we need the "Alternating Series Estimation Theorem" (p. 754):
- #27
- #34
- The alternating harmonic series is convergent
(Example 1, p. 753).
That being said, a theorem below does give us some help in determining the value of (or at least bounds on the value of) the series of a type called an "alternating" series. In particular, we want to look at alternating series like the one below:
So it turns out that if the terms are converging to 0, then the alternating sequence converges to a limit.
Now we usually write our alternating series in the following way, illustrated by Leibniz's test: we assume that the are positive, and the term
takes care of the "alternation". (Our textbook switches to
for the positive part of the term.)

Our textbook calls this the "Alternating Series Test" (p. 751). The "Furthermore" part our textbook calls the "Alternating Series Estimation Theorem" (p. 754).
- First, a definition:

- Series that converge absolutely, and
- Series that don't.


- Examples:
- #5, p. 761
- #12, p. 761
- It turns out that conditionally convergent series can have their terms rearranged to converge to any limit you like (let's take a look at "Rearrangements", on p. 761). Hmmm.... Is this the end of commutativity?!
- The Ratio and Root Tests
- There are two main tests for convergence of series in this section:

This result says that eventually the ratio of successive terms is effectively constant,
: the terms of the sequence approach a "common ratio" as
. What kind of series looks like that? A geometric series:
Examples:
- #2, p. 761
- #3, p. 761
The ratio test is effectively a self-referrential comparison test: we compare terms of
with other terms
(rather than with some other series).

This result says that eventually the absolute values of the terms are effectively equal to
: what kind of series looks like that? A geometric series!
No wonder the results of the tests look exactly the same.... Too bad we didn't just use the same letter for the limits in both cases!
Notice that, once again, limits of sequences plays an important role! Series are just sums of sequences, after all; we're focused on how terms behave (root test), how successive terms behave (ratio test), or how partial sums behave.
Examples:
- #7, p. 761
- #13, p. 761
- There are two main tests for convergence of series in this section: