Day 45 in MAT229

Last time

Next time

Today:

Announcements:
- Your exams are not going well. They're often far from perfect. That means I have to regrade them, for a grade (<100).
  Why didn't some of you check out the (pretty good) answers on the website?
  A good example is the discussion of errors in Problem 3. I've got two good discussions on there, in which the students discuss "size and sign" of the errors. Now I'm looking at "perfect" papers for which the answers are roughly "better methods give better answers". Blah!
  Didn't I tell you that problem 6 on the exam came almost straight from section 10.2?
  What are we missing here?
  The grader is definitely miffed, and you'll recall that rule one is "don't piss off the grader."
- Your 11.4 homework is returned:
  - 4: diverges by comparison with ${\frac{1}{n}}$
  - 20: converges, as we saw in class
  - 44: The easiest way to show this is graphically. We know that ${a_n}$ dominates ${\ln(1+a_n)}$ by examining the graphs of ${x}$ and ${\ln(1{+x})}$ for x positive:
    
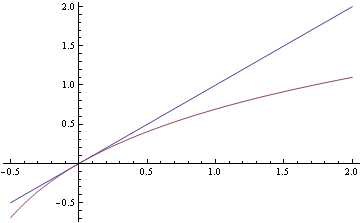
    Be careful to distinguish between terms of a series and the series itself.
- Your 11.5 homework is due today
- Today we're going to get into 11.7 for some cold convergence examples, and then start 11.8.
- Well, there's good news and there's bad news. The bad news is that we're not going to get famous....
Section 11.6: Absolute versus Conditional Convergence, and ratio and root tests
- First, a definition:
  
  Let's think of a couple of examples of
  - Series that converge absolutely, and
  - Series that don't.
- Examples:
  - #5, p. 761
  - #12, p. 761
  - It turns out that conditionally convergent series can have their terms rearranged to converge to any limit you like (let's take a look at "Rearrangements", on p. 761). Hmmm.... Is this the end of commutativity?!
- The Ratio and Root Tests
  - There are two main tests for convergence of series in this section:
    
    This result says that eventually the ratio of successive terms is effectively constant, $\rho$ : the terms of the sequence approach a "common ratio" as ${n\to\infty}$ . What kind of series looks like that? A geometric series:
    
    ${\sum_{n=0}^{\infty}\qquad{c}\rho^n}$
    Examples:
    - #2, p. 761
    - #3, p. 761
    The ratio test is effectively a self-referrential comparison test: we compare terms of ${a_n}$ with other terms ${a_{n+1}}$ (rather than with some other series).
    Here's a test that is also self-referrential, but only looks at a single term -- the root test:
    
    This result says that eventually the absolute values of the terms are effectively equal to ${|a_n|={L^n}}$ : what kind of series looks like that? A geometric series!
    
    ${\sum_{n=0}^{\infty}\qquad{L^n}}$
    Notice that, once again, limits of sequences plays an important role! Series are just sums of sequences, after all; we're focused on how terms behave (root test), how successive terms behave (ratio test), or how partial sums behave.
    Examples:
    - #7, p. 761
    - #13, p. 761
Section 11.7: Strategies for testing series
- Let's take a look at some problems. Pick examples from p. 764-765 which look interesting.
Section 11.8: Power series
- Summary:
  Now, rather than simply consider infinite sums of numbers, we're going to consider an infinite sum of functions in what are known as power series. They're like polynomials, but they don't have finite degree.
  The terms will be monomials -- functions with are simply constants times powers of x.
  Now we realize that, with functions for terms, each value of x specified gives rise to an infinite series, and we might immediately wonder if the series is convergent for a particular choice of ${x}$ .
  So what kind of function has an infinite number of terms? How do you evaluate such a thing? What kinds of function are these? It turns out that a lot of our old friends can be expressed this way
  ${F(x)={e^x}}$ , for example, as we've seen.
  Now what did we assert about ${F(x)={e^x}}$ ? That
  ${e^x=\sum_{n=0}^{\infty}{\frac{x^n}{n!}}}$
  For what values of x would this converge?
  
  Let's take a look at how well a truncated power series -- a partial sum -- approximates the real function.
  1. Graph ${e^x}$ on the interval [-2,2].
  2. Graph ${p_1(x)=\sum_{n=0}^{1}\frac{x^n}{n!}}$
  3. Graph ${p_2(x)=\sum_{n=0}^{2}\frac{x^n}{n!}}$
  4. Graph ${p_3(x)=\sum_{n=0}^{3}\frac{x^n}{n!}}$
  What do you see happening?
  
  Apply the ratio test for arbitrary x, and what do you discover?
  
  So ${F(x)={e^x}}$ presents us with a case where we have an "infinite radius of convergence".
  
  Interesting sidelight: you may have encountered Euler's Formula at some point in your life:
  
  ${e^{i\theta}=\cos(\theta)+i\sin(\theta)}$
  where ${i=\sqrt{-1}}$ . From this (and the power series for ${e^x}$ ) we can now deduce power series for the functions cosine and sine. Let's do that.
  Excuse me for saying, but this is very cool. It illustrates for you, as perhaps nothing ever has, the value of using imaginary (and complex) numbers.
  
  Let's look at an example where our radius of convergence is not so nice: consider ${F(x)=\frac{1}{1-x}}$ . One can show that
  
  ${\frac{1}{1-x}=\sum_{n=0}^{\infty}{\qquad{x^n}}}$ In fact we deduced this for a particular case when we looked at geometric series: that ${\frac{1}{1-r}=\sum_{n=0}^{\infty}{\qquad{r^n}}}$ But now we're talking about a function of x. One can think of x as representing allowable values of r (that is, values of r for which this geometric series converges). We know that this is for values of r such that .
  
  Now: for what values of x do you think that this will converge?
  
  Note that this is a variation on the theme of the ratio test: we don't consider the power terms, but only the coefficients.
- Examples:
  - What does Theorem 2 say will be the radius of convergence of the series for ${F(x)=\frac{1}{1-x}}$ ?
  - What about the endpoints?
  - How well do the truncated partial sum functions approximate ${F(x)=\frac{1}{1-x}}$ ?
  - #7, p. 769
  - #19
  - #27

Website maintained by Andy Long. Comments appreciated.
Updated on 09/30/2014 23:35:07