- If you didn't pick up your exam last time, it's in the envelope on my door.
- Prof. Steve Wilkinson is with you today, to work on the basics of
vectors and two important operations in vector calculus: the dot and
cross products.
- I'll be back on Thursday, at which time we'll have a review session for the comprehensive final. Come prepared with questions! You'll hopefully have begun preparing your 8.5x11 (inches!) sheet with all the magic formulas you need on it.
- Uniform Circular Motion is best understood using the concepts of vector geometry.
So are many other concepts from physics, where quantities have a direction and a "strength" -- a rocket in flight, for example. It is moving in a certain direction, and it has a speed, whose value can be represented by the length of a vector.
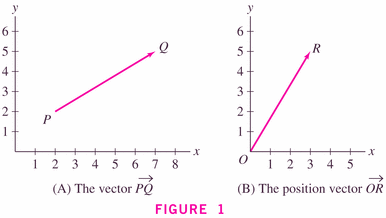
- vector: a quantity with length and direction:
- In uniform circular motion, we could represent the position of the bob by parametric equations
and
We then combine these into one quantity, the vector
.
- The three vectors that are (most) important in the physics
of circular motion are the vectors of
- position
- velocity
- acceleration
- position
- Animations, demonstrations:
- Uniform Circular Motion
- For all of the gory details, a nice layout of all the physics, and a cool (but scary) example, let's check out physclips -- the Australian dialect makes it more fun, too!
- vector: a quantity with length and direction:
- If a vector is in two-dimensions, then the length
is just given using the Pythagorean theorem formula:

For a vector given by
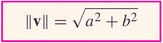
Hence in 3-d,
we have
or for
Obviously this can be generalized to vectors in four dimensions, five dimensions; even six dimensions. Maybe seven dimensions, too; or even n dimensions! (Especially important for you statisticians).
Examples:
- 3-D Point drawing instructions
- #1, p. 814
- #2
- #3
- #4
- #5
- #6
The equation for a sphere centered at the point (h,k,l) of radius r given in our text is
This is the set of points P at a distance of r from the point (h,k,l).
Examples:
- #12, p. 814
- #17
- #21
- #23-33 odd
- The vectors above are given with components:


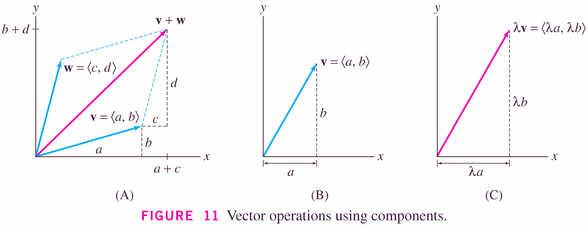
- Figure 11 illustrates the so-called parallelogram
rule:
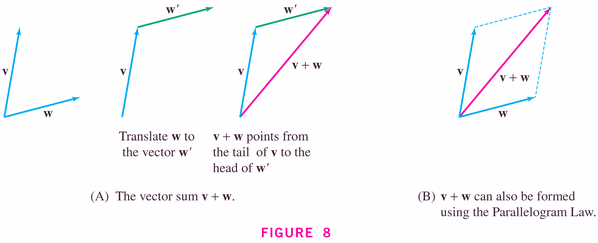
Examples:
- #5, p. 822
- #15
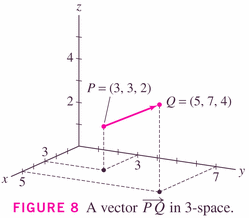
Here it is in three-space:
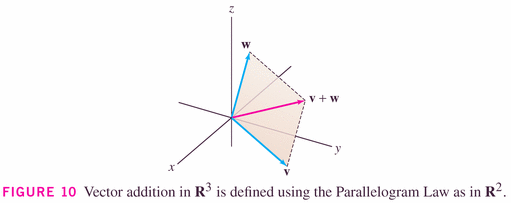
with the obvious changes to formulas because you now have three components, instead of two:
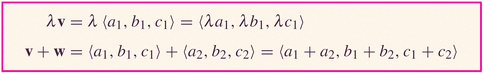
- Vectors with length 1 are special, called unit
vectors, and are important because they can be dedicated to
showing direction:
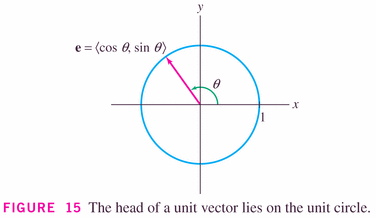
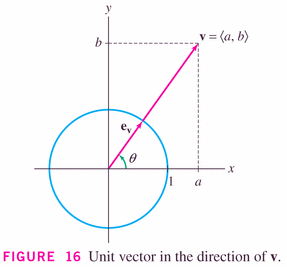
It's clear that we can turn any vector into a unit vector, by simply scaling it:

Examples:
- #23, p. 823
- #24
- We use special components and the parallelogram rule to
write each vector in terms of a basis of vectors (equal
in number to the dimension of the space): for example, in
two-space, the usual basis is given by the two (perpendicular)
vectors denoted i and j:
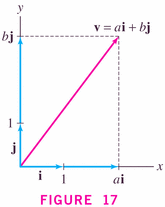
and, in three-space,
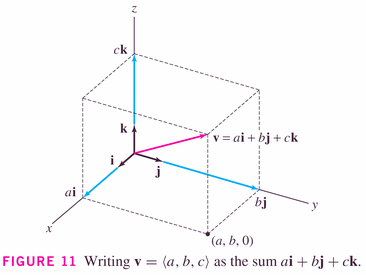
- Theorems:

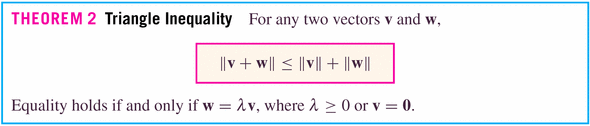
The Triangle inequality basically says that the diagonal of a parallelogram is shorter than or equal to the sum of the two sides:
"The shortest distance between two points is a straight line." In the case of Figure 17 (for vectors at right angles to each other)

and the only time you'll have equality is when either a or b is zero.
Examples:
- #29, p. 823
- #31
- #42, p. 824
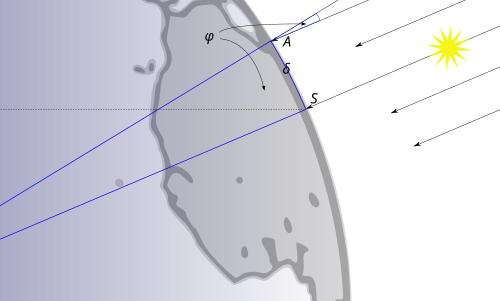
- An example problem, in which we need a "shadow casting" function: Eratosthenes and the calculation of the radius of the Earth.
-
Now let's think a little more about how we resolve the vector forces into components: we'll find it convenient to define a product of two vectors as follows:

(how would you define this for vectors in two-space?). It's just component-wise multiplication, and we add up the results.
examples:
- #1, p. 830
- #5
- #11
It turns out that

where

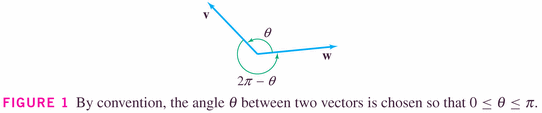


Otherwise, the angle is acute. examples:
- #15, p. 830
- #17
Finally then, we can put it all together to get this:
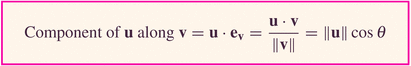
In a way, this is the "shadow" of vector u along v's direction (notice that v's length has been accounted for, by using the unit vector in the v-direction).
- Additional examples:
- #51, p. 831
- #57
- The next product we'll find convenient to define is the cross
product, which is a product of two vectors resulting in a third vector,
which juts into the space perpendicular to which the two vectors live.
It is only defined (and useful) in three-space, which makes it somewhat unusual (the dot product exists and is useful in any dimensional space).
The cross product is linear in its components: that is,
This means that we can define it on the unit vectors in three space, and then deduce it using the component-wise definition of a three-vector.
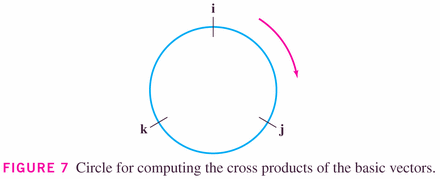
- #5, p. 838
Now: here are the important geometric (rather than simply algebraic) properties of this product:

for the dot-product, it's the cosine; for the cross-product, it's the sine.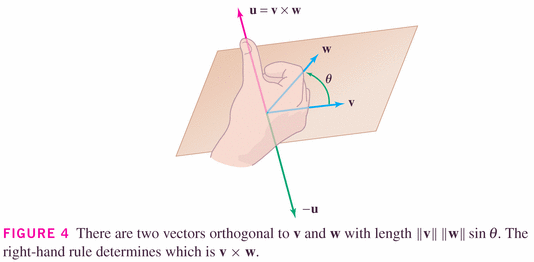
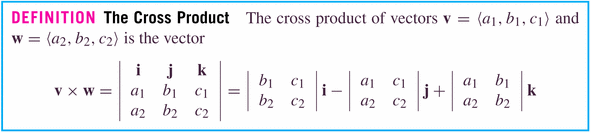
The "absolute values" in this case represent determinants, which, for a 2x2 system with first row a, b and second row c, d is given by
. So the computation above works out to
Example:
- #7, p. 838
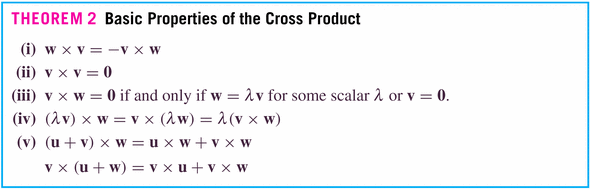
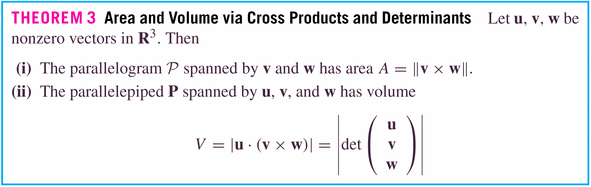
Examples:
- #15, p. 838
- #33, p. 839
- Torque: #39
- Torque: #41