Day 15, Mat129: Calculus I

Last time:

Next time:

Today:

Announcements
- Your tests are returned.
  - The exam
  - The distribution
  - The key
  - The curve: add 6 to your raw score, the divide by .6 for your "percentage".
  - Feel free to come talk to me about your test if you wish.
  - More of you could benefit from
    - using the calculus lab and/or visiting me during office hours;
    - taking notes (you can't expect to get calculus via osmosis);
    - and actually memorizing important things (e.g. the MIDIC). Googling is simply not enough. If you don't have a storehouse of ready, useful information, then I can probably outsource your job -- although I wouldn't -- but someone else will.
- Today we're going to continue looking at derivatives of trig functions (section 2.4), in particular sines and cosines; review a few more derivative laws, and then push on into 2.5: the chain rule.
- I forgot to announce that I was picking up the homework on Friday, so if you were in class on Friday, but left before turning it in, then you may. (That was section 2.2.)
- You have a homework to hand in Wednesday, and Imath due Wednesday.
- I've assigned new homework to turn in next Monday, and two IMath assignments for sections 2.3 and 2.4.
Back to Section 2.3: Differentiation formulas:
- Last time we proved several rules for differentiating certain functions:
- Rules that help us avoid having to use the definition each time
  - The constant multiple rule (makes sense)
    
    $(cf(x))'=cf'(x)$
  - The sum rule
    works as we'd hope: "The derivative of a sum is the sum of the derivatives."
    
    $(f(x) + g(x))'=f'(x)+g'(x)$
  - The power rule (via dominoes -- i.e., mathematical induction -- or via the binomial theorem)
    
    $(x^n)'=n x^{n-1}$
  - NOTE: at this point we have all the rules necessary to differentiate all polynomials, without needing to resort to the definition!
    The derivative of the monomial $x^n$ is $nx^{n-1}$, and
    The derivative of the monomial $c x^n$ is $nc x^{n-1}$ (by constant multiple).
    A polynomial is just a sum of these. So we apply the sum rule, and the power rule, and the constant multiple rule to the flight of the eraser, to get
    $s'(t)=(at^2+bt+c)'=2at+b$
    and
    $s''(t)=(2at+b)'=2a$
- Other rules:
  - The product rule (doesn't work the way we'd hope):
    
    $(f(x) \cdot g(x))'=f'(x)g(x)+f(x)g'(x)$
  - The quotient rule:
    
    low d high minus high d low,
    over the denominator squared they go.
    $\left(\frac{f(x)}{g(x)}\right)'=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}$
Examples:
- #13, p. 136
- #22, p. 136 (expand first, or treat as a product -- which does Mathematica do?)
- #48, p. 137
- #58, p. 137

Today we'll continue our attack on Section 2.4: Derivatives of trig functions.

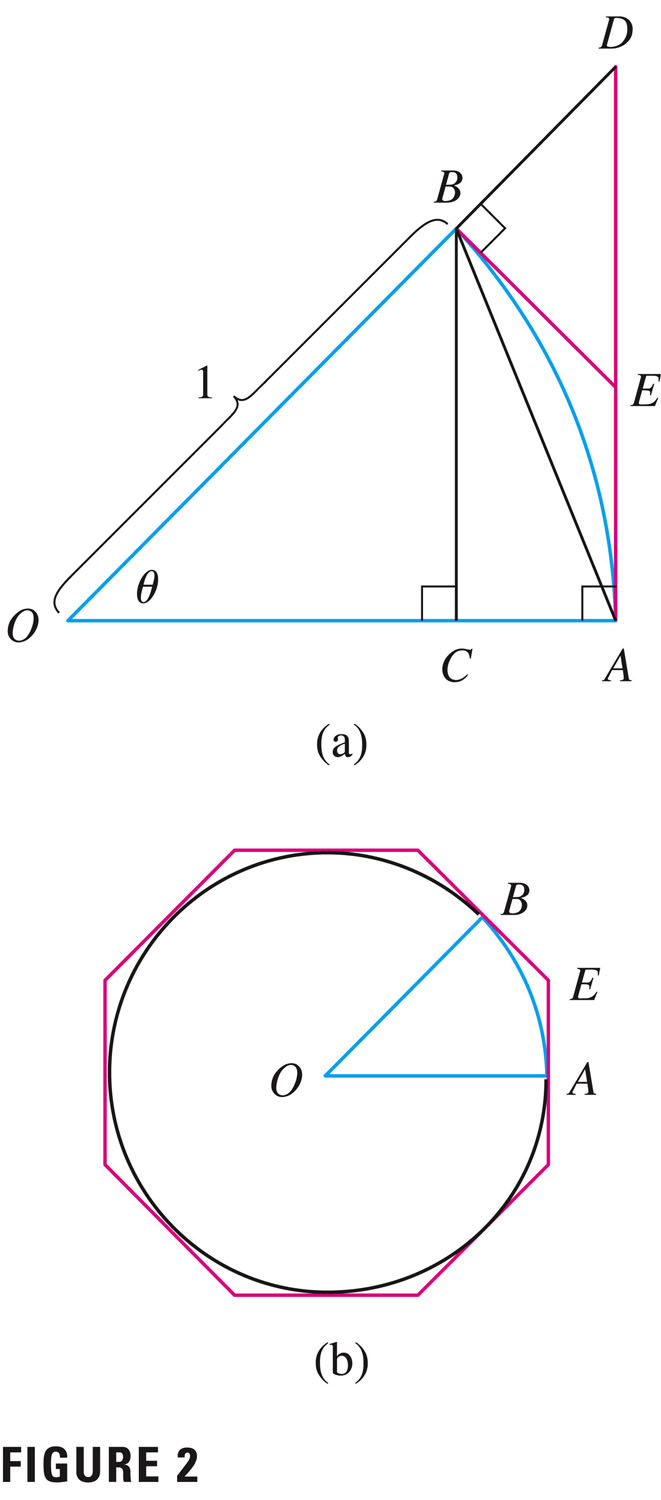
The derivatives of trig functions rely on some basic understanding of the circle.
- Radian measure: $RADIANS=\frac{2\pi}{360}DEGREES$. In calculus, we almost always use radians.
- Length of a sector, related to angle $\theta$ subtending and radius $r$:
  Arc Length: $L = \theta r$
- Definitions of the trig functions, as functions of $x$, in radians (which is how we think about them in calculus):
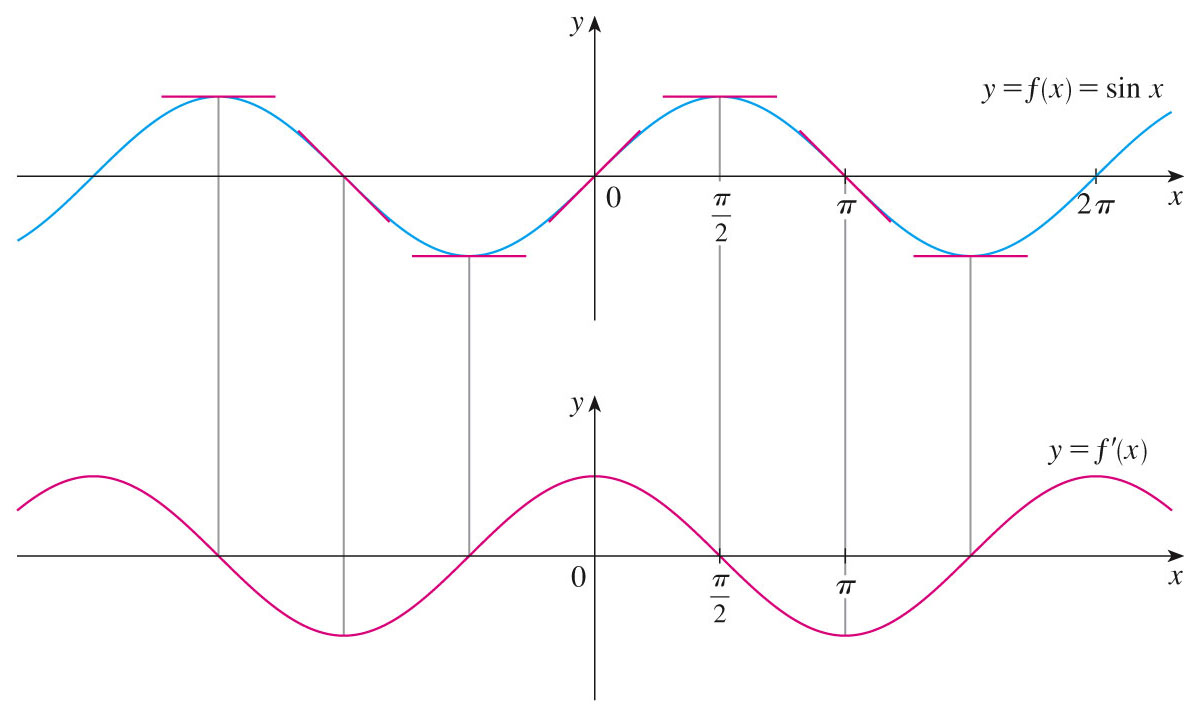
We will derive the derivative of the sine function from the limit definition of the derivative (although we can see the derivative graphically above).
There are exactly three important trig identities one needs to know (all the others can be derived from these three):
- The Pythagorean theorem:
  
  $\sin^2(x)+\cos^2(x)=1$
- The sine of a sum:
  
  $\sin(a+b)=\sin(a)\cos(b)+\sin(b)\cos(a)$
- The cosine of a sum:
  
  $\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$
So let's see how to derive the derivative of the sine from the MIDIC -- the limit definition of the derivative -- using the second of these identities.
Then the derivative of the cosine can be derived by simply shifting the sine function, and using the second trig identity above.
Let's see how that's done.....
Examples:
- Derivative of tangent (use the quotient rule, of course!)
- Fourth derivatives of sine, cosine
- #7, p. 146
- #26
- #35
- #49

Now on to Section 2.5: The Chain Rule

The chain rule is so critically important because of the importance of compositions of functions: for $F(x) = f(g(x))$,

$F^\prime(x) = f^\prime(g(x))g^\prime(x)$
I personally think this to myself: "f prime of stuff times the derivative of the stuff"; or "f prime of stuff times stuff prime."

$F^\prime(x) = f^\prime(stuff)stuff^\prime$
You can see that the rule is fairly simple, once you've identified the composition -- that is, once you've torn apart $F$ to find $f$ and $g$.
Take a look at a file from my pre-calc class if you need to review compositions. They're tremendously important (there's a composition in the MIDIC).
The difficulty is often identifying the composition. We'll try some easy ones first, then get to some ugly ones.
We won't prove the chain rule, but we can motivate it using the limit definition of the derivative. Everything comes from that, but this derivation is a little bit complicated. Let's focus on identifying the proper compositions.
Examples:
- #9, p. 154
- #16
- #29
- #42
- #77
A Chain Rule tutorial
A sample problem involving compositions: model the seasonal variation in Keeling's CO2 data:
1. If time were measured in years from January, would
  
  $V(t)=A\sin(2\pi{t})$
  be a good model for the Annual Cycle? In what way is this a composition? What are the functions involved, and to what families do they belong?
2. What would be a good choice for the parameter $A$?
3. What kind of function would this variation term be combined with (and how) to create a model for Atmospheric Carbon Dioxide?

Website maintained by Andy Long. Comments appreciated.