- We'll meet in the lab on Friday
- We'll have a quiz today at the end of the hour.
- You have a homework to hand in today (and IMath due tonight).
- The derivatives of trig functions rely on some basic
understanding of the circle.
- Radian measure: $RADIANS=\frac{2\pi}{360}DEGREES$. In calculus, we almost always use radians.
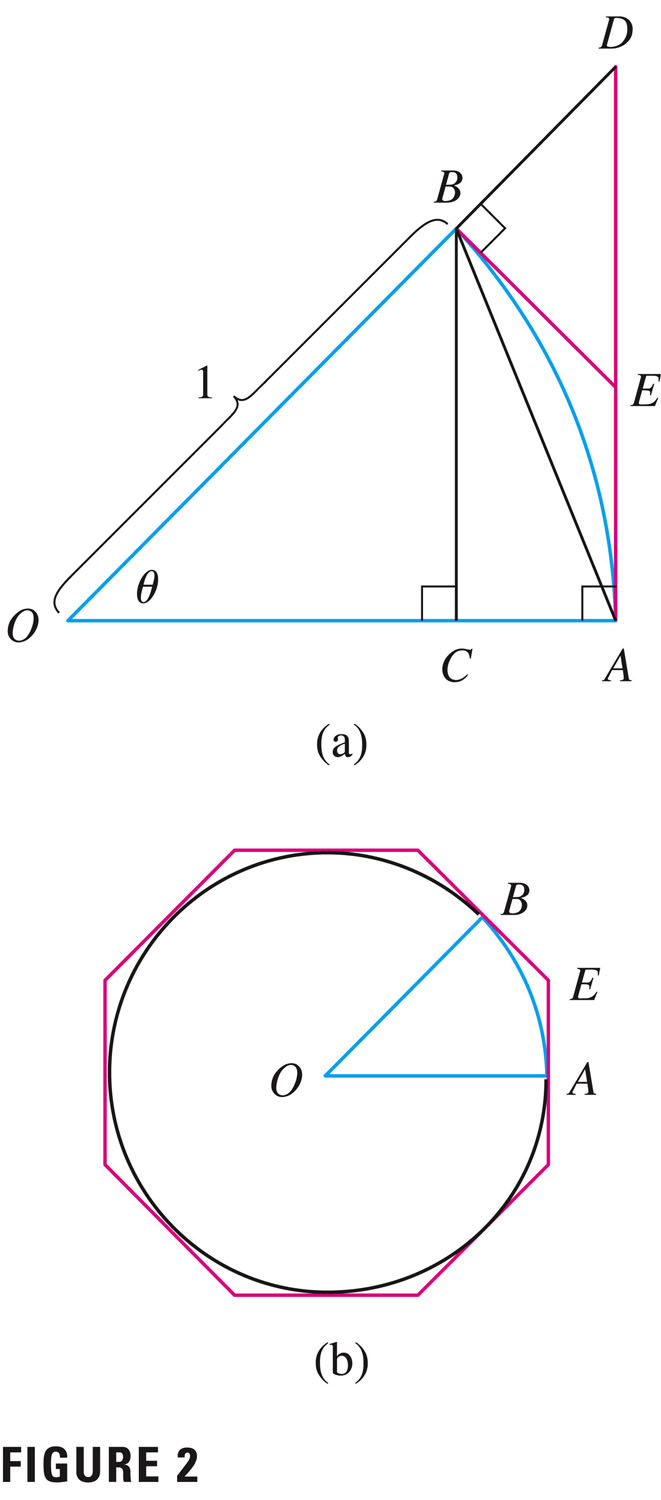
- Length of a sector, related to angle $\theta$ subtending
and radius $r$:
Arc Length: $L = \theta r$
- Definitions of the trig functions, as functions of $x$, in radians (which is how we think about them in calculus):
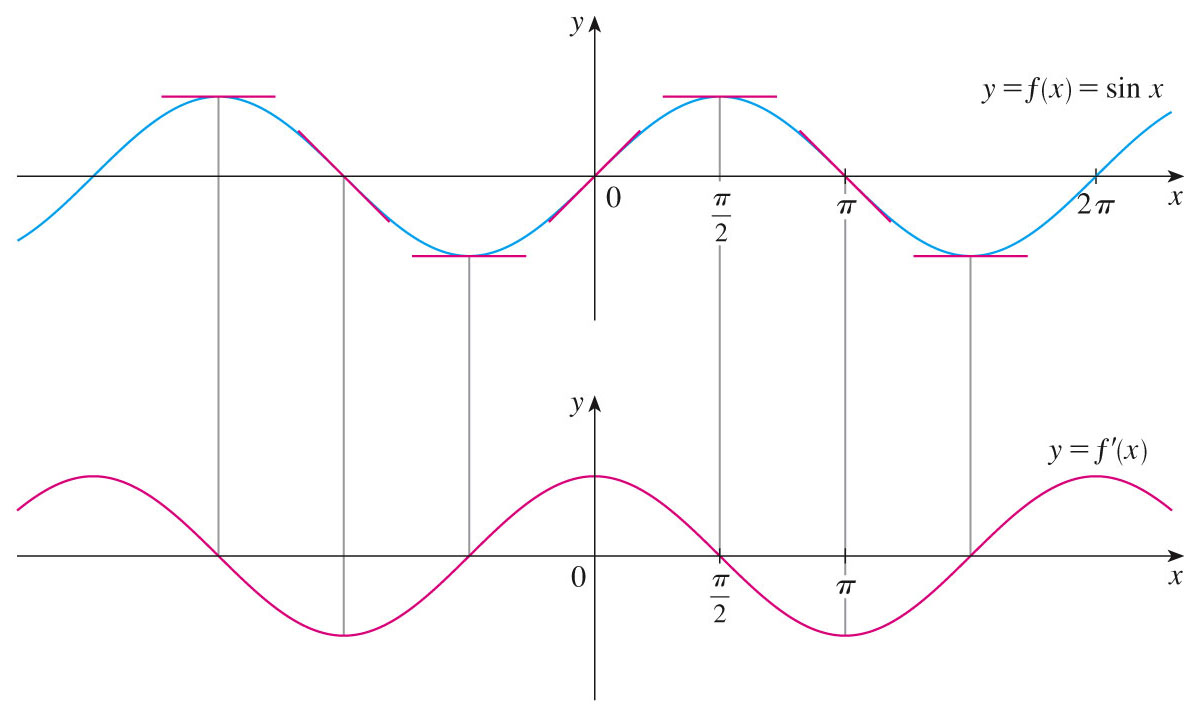
We will derive the derivative of the sine function from the limit definition of the derivative (although we can see the derivative graphically above).
There are exactly three important trig identities one needs to know (all the others can be derived from these three):
- The Pythagorean theorem:
$\sin^2(x)+\cos^2(x)=1$ - The sine of a sum:
$\sin(a+b)=\sin(a)\cos(b)+\sin(b)\cos(a)$ - The cosine of a sum:
$\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$
So let's see how to derive the derivative of the sine from the MIDIC -- the limit definition of the derivative -- using the second of these identities.
Then the derivative of the cosine can be derived by simply shifting the sine function, and using the second trig identity above.
Let's see how that's done.....
- Examples:
- Derivative of tangent (use the quotient rule, of course!)
- #7, p. 146
- #26
- #35
- #49 (and fourth derivatives of sine, cosine)
- The chain rule is so critically important because of the
importance of compositions of functions: for
$F(x) = f(g(x))$,
$F^\prime(x) = f^\prime(g(x))g^\prime(x)$ I personally think this to myself: "f prime of stuff times the derivative of the stuff"; or "f prime of stuff times stuff prime."
$F^\prime(x) = f^\prime(stuff)stuff^\prime$ You can see that the rule is fairly simple, once you've identified the composition -- that is, once you've torn apart $F$ to find $f$ and $g$.
Take a look at a file from my pre-calc class if you need to review compositions. They're tremendously important (there's a composition in the MIDIC).
- The difficulty is often identifying the composition. We'll try
some easy ones first, then get to some ugly ones.
We won't prove the chain rule, but we can motivate it using the limit definition of the derivative. Everything comes from that, but this derivation is a little bit complicated. Let's focus on identifying the proper compositions.
Examples:
- #9, p. 154
- #16
- #29
- #42
- #77
- A Chain Rule tutorial
- A sample problem involving compositions: model the seasonal variation in Keeling's CO2 data:
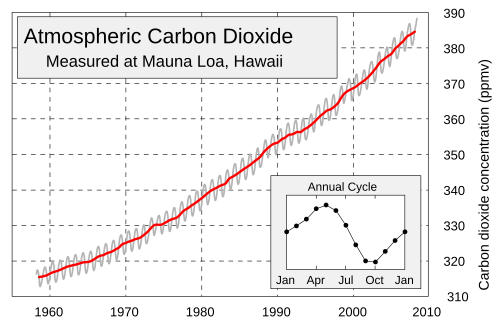
- If time were measured in years from January, would
$V(t)=A\sin(2\pi{t})$ be a good model for the Annual Cycle? In what way is this a composition? What are the functions involved, and to what families do they belong?
- What would be a good choice for the parameter $A$?
- What kind of function would this variation term be combined with (and how) to create a model for Atmospheric Carbon Dioxide?
- If time were measured in years from January, would