- Your little assignment is due today (compute a regression equation by hand for the Keeling data).
- Also a reminder that your mini-projects #1 are due Friday. Remember
that this is a group project, and I just want one report per
group. These reports will be made available to all, because
we're going to next assemble all the towns into one single model
for all of Togo; so I'll need an electronic copy to post.
If your group has any questions, feel free to stop by and talk to me!
Monday's "first contact" introduced vector and matrix notation, and a few important operations (e.g. transpose and inverse). But the details will be left to a linear algebra course!
Matrices will be important in other models we consider, so let's be glad we meet them early.
- We will look at some of the functions from the "Bestiary" which can be linearized, meaning that we can use linear regression to estimate their parameters.
- We will look into how to handle model fit for non-linear models (so non-linear regression); and then
- We'll take a look at some examples, to see how this is useful!
- So we'll wrap up the linear algebra derivation
today. Our objective is to show where the results of
linear regression programs come from.
- Then we'll check
the results using Mathematica, to see that we get
the same fit to Stewart's Keeling data as we did using
Mathematica's LinearModelFit.
How would you adjust things to get the quadratic fit? Let's try!
- At the end of that Mathematica file is a set of diagnostics. We'll
talk about those, after verifying that the linear algebra works
for determining $a$ and $b$.
- Regression Diagnostics: Polya's "evaluate" step.
There are three things I always consider about a model:
- Graphical check of Fit and Residuals - is there a
pattern to the residuals? If so, we go back to
the model-building step....
- residual "errors" are supposed to be "iid" -- independent and identically distributed (and we hope for normally distributed).
- Hopefully the residuals are not clustered, nor wildly different in size, and,
- if you graph the residuals as a histogram, you get something resembling a normal distribution (bell-shaped curve).
- $R^2$: how much variation does my model explain?
- We break variance down into two parts: a fraction due to the model, and the residual.
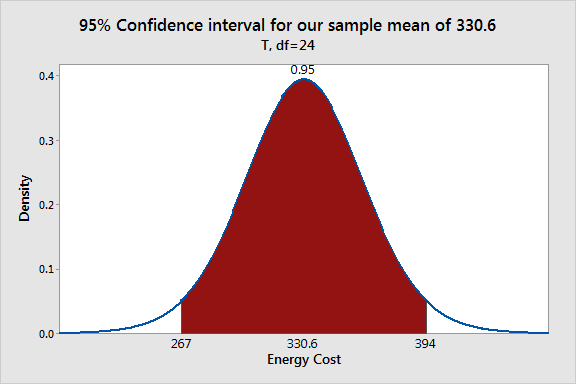
- Confidence intervals for parameters (essentially
equivalent to p-values, but perhaps more
informative).
The standard errors of the parameters pop out of the inverse matrix we compute, multiplied by the mean SSE. Once we have those, we have everything we need for confidence intervals.
We're often interested to know whether we can exclude a certain value from a confidence interval -- e.g., can we conclude that the slope parameter $b$ in a linear regression $y(x)=a+bx$ is not 0? If so, we conclude that there is a non-zero slope, and the model suggests that $x$ drives values up or down, depending on the sign of $b$.
- Graphical check of Fit and Residuals - is there a
pattern to the residuals? If so, we go back to
the model-building step....
- Links:
- Using Mathematica's LinearModelFit to find linear
models that fit Stewart's Keeling data
- An extract from Curve
Fitting via the Criterion of Least Squares, by John
Alexander. A bit old-fashioned, but it's got all the
major ideas, and some nice examples.
Alexander also illustrates that one cannot simply invert the regression equation $y=a+bx$ to get the regression equation $x=\frac{y-a}{b}$. So it really matters in linear regression which variable is considered "independent" and which is considered "dependent".
- My linear algebra derivation.
- Using Mathematica's LinearModelFit to find linear
models that fit Stewart's Keeling data