- We're in week 10 of the semester, about 2/3 of the way in.
I hope that you enjoyed some break in your "Spring Break". This is that time when I personally need a little revitalization; and a week off usually does it. I'm not sure that a "long weekend" is going to have the same effect.
- Your symmetry homework hasn't been graded yet.
I do have to get the midterm grades in by tomorrow. I try to get every grade possible in so that I can give my most honest assessment. We'll see if I can get the symmetry one done today.
So you'll have those midterm grades by tomorrow morning (Tuesday). I try to err on the realistic side....
- You had a couple of readings from Strogatz. We didn't get
to those last time, so I'm going to get to a little more on
those today.
- Materials for today:
- Here is our video:
- Part III (the other two parts came last time).
- The associated work by hand
- Here is our video:
The Bridges of Konigsberg problem: "is it possible to set off and walk around Konigsberg crossing each bridge exactly one?"
- Euler's solution:
- Konigsberg: To be traversable, there must be at most two vertices of odd degree.
- Euler noticed the hand-shaking theorem: in any graph, the number of vertices with odd degree must be even.
- Interestingly enough, we turned the Platonic solids into graphs, and then asked which can be traversed without backtracking? (Here they are again)
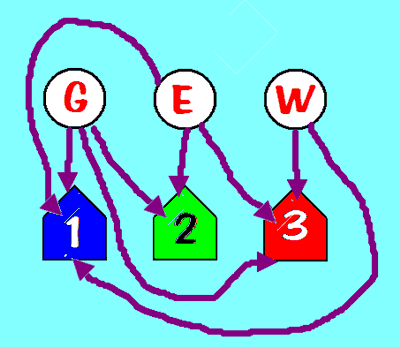
- Graphs may be directed: for example, in Strogatz's "Group
Think", he considers how to treat your mattress:
(Did you know that you should "spin in the spring, flip in the fall."?)
There is a certain amount of curious algebra here:
HR=RH=V means that
- a horizontal flip followed by a rotation is equivalent to
- a rotation followed by a horizontal flip is equivalent to
- a vertical flip.
Not everything "commutes" (like $HR=RH$). There is a famous story told by Murrey Gell-Mann: "It occurred to me that I could try MIT first, and then commit suicide, whereas I couldn't do things in the reverse order: if I committed suicide I could not then afterwards try MIT: the two operators didn't commute."
- They may also be labelled, and weighted, as in
Strogatz's article on "The Enemy of My Enemy":
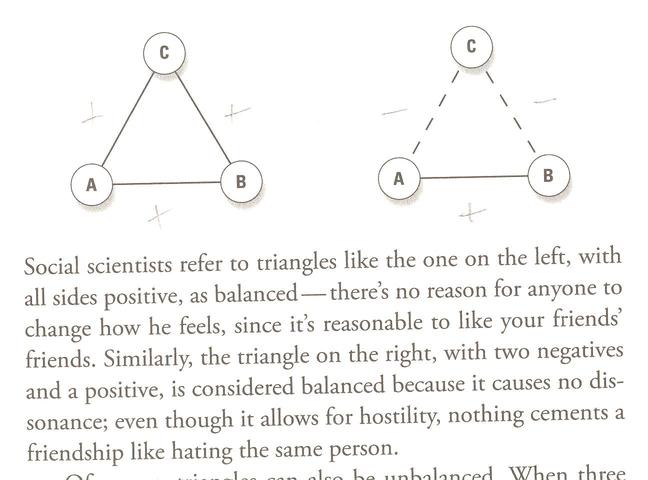
"The enemy of my enemy is my friend." -- 'The corners signify people, companies or countries, and the sides connecting them signify their relationships, which can be positive (friendly, shown here as solid lines) or negative (hostile, shown as dashed lines).'
'Social scientists refer to triangles like the one on the left, with all positive, sides balanced, -- there's no reason for anyone to change how they feel, since it's reasonable to like your friend's friends. Similarly, the triangle on the right, with two negatives and a positive, is considered balanced because it causes no dissonance; even though it allows for hostility, nothing cements a friendship like hating the same person.'
'Leaving aside the verisimilitude of the model, there are interesting questions here of a purely mathematical flavor. For example, in a close-knit network where everyone knows everyone, what's the most stable state? One possibility is a nirvana of goodwill, where all relationships are positive and all triangles are balanced. But surprisingly, there are other states that are equally stable. These are states of intractable conflict, with the network split into two hostile factions. All members of a given faction are friendly with one another, but antagonistic toward everybody in the other faction. (Sound familiar?) Perhaps even more surprisingly, these polarized states are the only states as stable as nirvana. In particular, no three-party split can have all its triangles balanced.'
- One focus of this reading is negative numbers. It
was the Indians (of Asia) who put negative numbers on a
firm foundation (as well as zero), in about the 6th
century AD.
"...you can't see negative 4 cookies and you certainly can't eat them -- but you can think about them...." ("and you have to", says our author).
- One of the confusing aspects of negative numbers
from Strogatz's perspective is that the product of two
negative numbers is a positive number.
- But then Strogatz goes on to use the context of
social interactions (negative and positive) to discuss
how we maintain stable relationships.
And the key to understanding stability in three-way social relationships is that the product of two interactions (signified by either +1 or -1) must be equal to the other: so that if two legs are positive, the third in the triangle must be positive; if one leg positive, and the other negative, then the third leg must be negative as well.
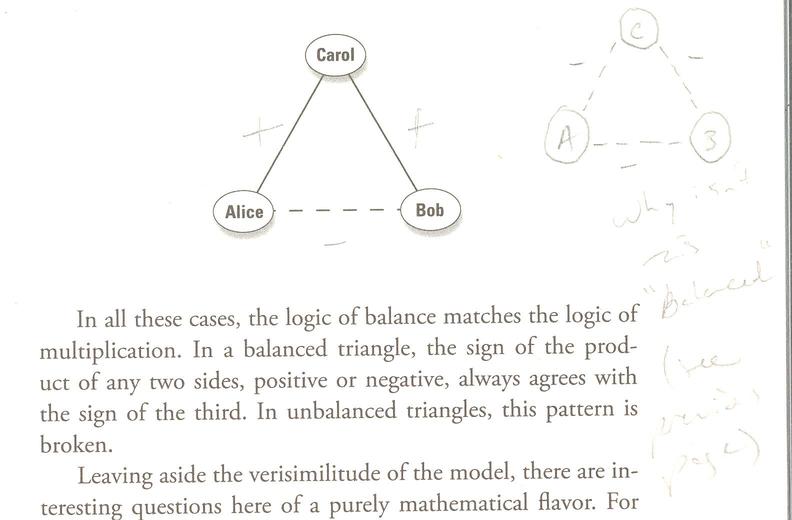
Strogatz sums up the second case above in the familiar saying that "The enemy of my enemy is my friend".
The following (two) graphs are unbalanced:
Finally Strogatz shows how historical relationships settled down into this pattern of stability: in "...the run-up to World War I. The diagram that follows shows the shifting alliances among Great Britain, France, Russia, Italy, Germany, and Austria-Hungary between 1872 and 1907."
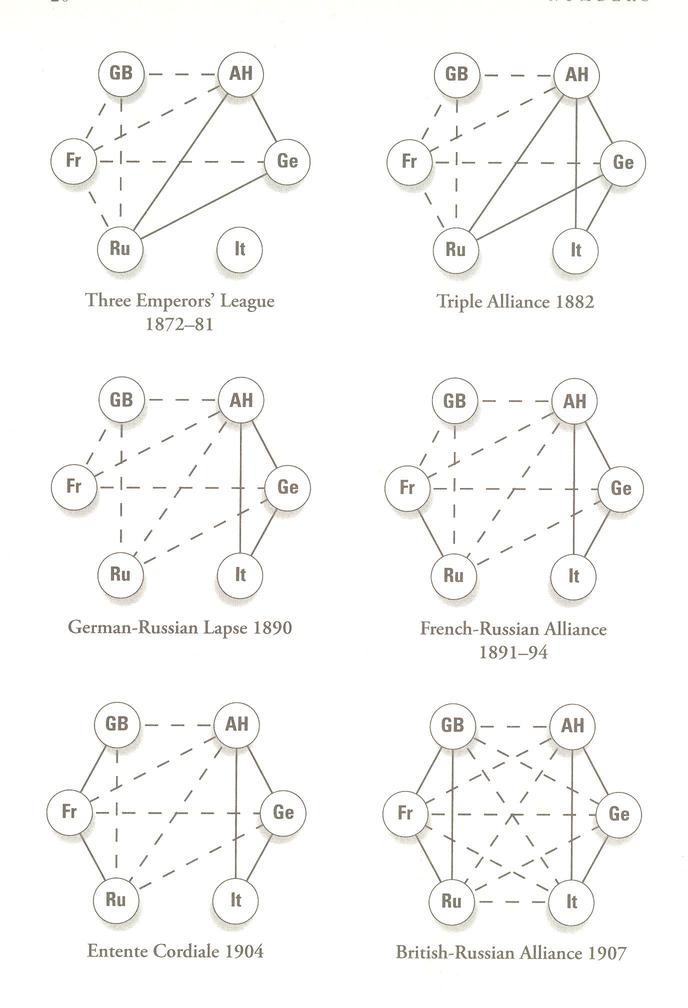
The bottom right graph (complete!) is the only stable configuration, "...balanced, but on the brink of war."
- One focus of this reading is negative numbers. It
was the Indians (of Asia) who put negative numbers on a
firm foundation (as well as zero), in about the 6th
century AD.
- You've
probably been making graphs for a long time.... (the pentagram)
- Graphs don't change by bending edges, but breaking them or
detaching edges from their vertices (and hence creating new vertices)
gives new graphs.
- A graph is simple if it doesn't have any loops (edges connected
from a vertix to itself), or multiple edges with the same two vertices.
- Exercise: Let's draw all the simple graphs with three vertices.
- A cycle is a route from a node back to itself that doesn't retrace steps.
- One of these graphs is a tree: a graph that has no cycles.
- Where have we seen trees used before?
- Duality -- again!
- Exercise: How about all
the simple graphs with four vertices. (These are different from the
Facebooks, because there we distinguished vertices -- here we use
symmetry, treating all vertices as the same.)
- Have you ever seen any of these before? Could we give any of them names?
- Finally I just want to show you all
the simple graphs with five vertices. I'm really proud of this creation, which is as close to art as I come! :)
- Planar graphs are graphs that can be drawn such that no two edges
intersect. Every Platonic
graph can be drawn this way, so they are planar graphs.
- Complete graphs are simply graphs with connections between
every pair of vertices (but no loops).
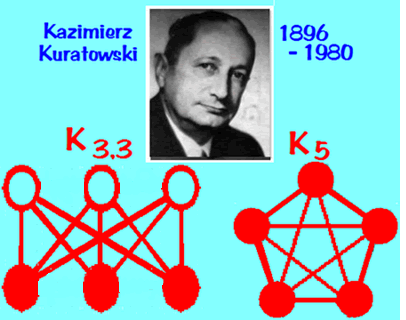
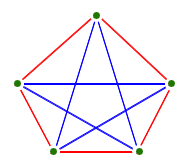
- Exercise: Let's see if we can show that the complete graph
with five vertices is not planar:
- We can show that the complete graph with four vertices is planar.
- Why not? What happens?
- The three utilities and three houses graph is not planar:
- Any non-planar graph has a copy of one of these two graphs
in it somewhere, as a subgraph:
- Graphs don't change by bending edges, but breaking them or
detaching edges from their vertices (and hence creating new vertices)
gives new graphs.
