Day 18, MAT115

You might use symmetry when you're drawing your complete graphs, because every vertex is the same as every other vertex; every edge is the same as every other edge.

1. Here is our video:
   1. Part I (the end of graphs!).
   2. Part II (Mobius bands).
   3. The associated work by hand

• Last time we looked at planar graphs (as well as some applications of graphs). I introduced planar graphs as graphs that can be drawn such that no two edges intersect. Edges only intersect at vertices.

  We noticed that every Platonic graph can be drawn this way, so they are planar graphs.

  We talked last time about "Euler paths" -- those graphs which can be drawn completely without crossing any edge more than once (the Konigsburg bridge problem). Only one of the Platonic solid graphs has an Euler path (which one? how did we know?).

  

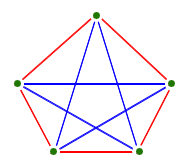
• We talked about how the complete graph with five vertices (which we call $K_5$) is not planar:
  

• Also how the three utilities and three houses graph (it's called the bi-partite graph $K_{3,3}$) is not planar. Here it is with one edge yet to draw: the edge which connects the water (W) to house 2:
  

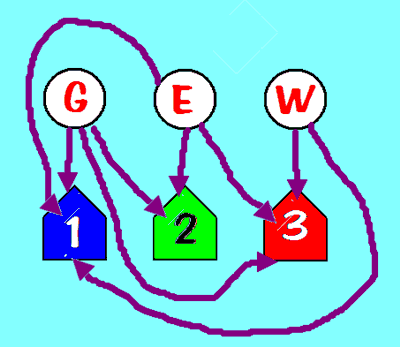
  Try as you might, you can't hook the water up to house 2 without crossing one of the edges.

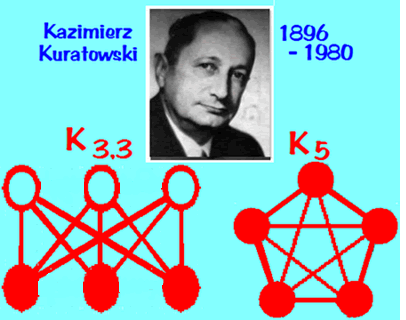
  You can't draw either of those graphs without some false intersections, and it turns out that every planar graph contains a subgraph that looks just like one of these (this is Kuratowski's theorem):

  

• It turns out that planar graphs have an interesting property that Euler also noted (he noticed a lot of things!): if you count up the number of vertices ($n$), and edges ($a$), and regions ($r$), you find that \[ r - a + n = 2 \] This is called Euler's formula. Note that the "outside region" that contains the graph is also counted as a region!

  Let's check and verify Euler's formula for some planar graphs:

  

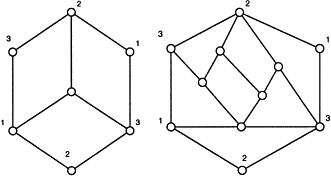
  Note: if you're dealing with a planar graph drawn with false intersections, then you have to remove false intersections before you begin; otherwise you'll get some "false regions!".

• I'm assigning you another video by Vi Hart to watch (see the assignments page). She does such a marvelous job of introducing you to some interesting ideas of both graphs and knots, which is upcoming!

  But I want to show something interesting from the video, and you'll be asked to do this for homework. I think she calls it a "squiggle graph".

  Draw a "squiggle" on a sheet of paper: don't lift your pencil, and in the end your squiggle should close back on itself. When you're done, start filling in "regions", so that you

(Graphs is the last topic that will be on the upcoming exam: you won't have any knots or links on the exam.)

• Mobius bands are a part of geometry, but relate to a special area called "topology" -- the study of form and shape.

  The Topologist's favorite riddle: What's the difference between a donut and a coffee cup?

  Answer: There isn't any! (to a topologist....)

• What is a Mobius band?
  • Let's make some!
  • A mobius band is made from a regular band using only a single twist.
  • By the way, did you know that there are two different Mobius bands? They're mirror images of each other! (Symmetry, again....)
    • Make one of each!
  • Properties of a mobius band:
    • A mobius band has only one side.
    • A mobius band has only one edge.

• Cutting a band:
  • What happens when you cut a mobius band "in half"? Check out a bug on a band....
  • What if you cut it into "thirds"?

• Applications of Mobius bands:
  • Conveyor belts
  • Kazakhstan's National Library in Astana
  • Recycling Topology:
    • The official recycling symbol is mobius, but over time an alternative has crept in:
      

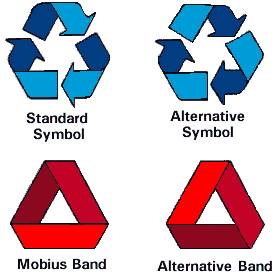
    • Mobius, or only Seemingly Mobius?
    • My dad loved mobius bands so much....
    • a history of the recycling symbol (and an AARP article on the history of the creation of the recycling symbol).
  • A joke: "Why did the chicken cross the Mobius band?"