- Your Egyptian Division has been graded (here's a key).
- Your symmetry homework was due last night, and will hopefully be
graded soon.
- You had a couple of readings for today. We're going to get to
those today.
- Materials for today:
- Here are a couple of videos:
- Here are my Euler notes:
-
The Platonic
solids possess a great deal of symmetry: they're super-symmetric
solids.
A cube is an example of a Platonic solid. It's the one we're most familiar with; although anyone who's played Dungeons and Dragons knows these solids from the shapes of the dice used.
A Platonic solid is a solid for which
- All faces are congruent (identical) convex regular polygons, and
- Each face, each edge, and each vertex is exactly equivalent to every other face, edge, or vertex (respectively).
And here they are!
The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia! Tetrahedron Hexahedron
or CubeOctahedron Dodecahedron Icosahedron 




fire earth air universe water Fig. 4.6 The platonic solids have been found living in the sea. The tetrahedron, somewhat rounded as if from internal pressure, is embodied in a protozoan called Callimitra agnesae, the cube is Lithocubus geometricus, the octahedron Circoporus octahedrus, the dodecahedron Circorrhegma dodecahedrus, and the icosahedron Circognia icosahedrus.
- Last time we filled in the following table (using symmetry!):
# of Vertices Edges Faces faces at each vertex sides at each face Tetrahedron 4 6 4 3 3 Cube 8 12 6 3 4 Octahedron 6 12 8 4 3 Dodecahedron 20 30 12 3 5 Icosahedron 12 30 20 5 3 What conclusions can we draw from this data? Is there a pattern? (Of course there is!:) The pattern leads to the concept of "Duality":
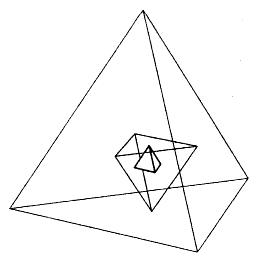
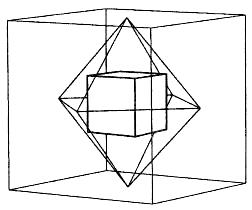
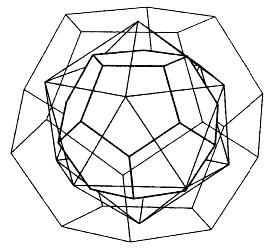
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.


"In the Hindu tradition, the icosahedron represents purusha, the male, spiritual principle, and generates the dodecahedron, representing prakriti, the female, material principle."
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.
- How can we draw the Platonic solids on a sheet of paper? We project them onto the paper.
- The cube you've undoubtedly done before.
- The tetrahedron can be drawn to be a "distorted" Mercedes symbol
- Here's the complete set.
- The Bridges
of Konigsberg problem: "is it possible to set off and walk around Konigsberg crossing each bridge exactly one?"
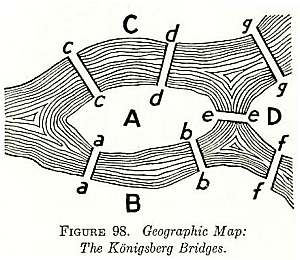

- Solved by Euler
(1735), the beginning of graph theory.
- We've already talked about graphs a little bit,
when we created "Facebooks".
- As a reminder (and perhaps a little more rigor)
Graphs are made up of vertices (points) and
edges that connect the vertices. More formally,
a graph is defined as
- A collection of points, called vertices.
- A collection of edges, each of which connects two vertices.
- a set of rules, one for each edge, telling how each edge is connected to its pair of vertices.
- The degree of a vertex is the number of edges coming into it. (We saw that this was a useful organizing tool when constructing the Facebooks, using symmetry.)
- We've already talked about graphs a little bit,
when we created "Facebooks".
- Euler's solution:
- Konigsberg: To be traversable, there must be at most two vertices of odd degree.
- Euler noticed the hand-shaking theorem: in any graph, the number of vertices with odd degree must be even.
- An alternative
solution (thanks to spiked math)
- Which of the Platonic solid graphs can be traversed without backtracking? (Here they are again)
- Solved by Euler
(1735), the beginning of graph theory.
- You've
probably been making graphs for a long time.... (the pentagram)
- Graphs don't change by bending edges, but breaking them or
detaching edges from their vertices (and hence creating new vertices)
gives new graphs.
- A graph is simple if it doesn't have any loops (edges connected
from a vertix to itself), or multiple edges with the same two vertices.
- Graphs may be directed: for example, in Strogatz's "Group
Think", he considers how to treat your mattress:


(Did you know that you should "spin in the spring, flip in the fall."?)
At right he develops a graph from an amusing story about Nobel-prize winning physicist Richard Feynman, and how he got a draft deferment.
The army psychiatrist questioning him asked Feynman to put out his hands so he could examine them. Feynman stuck them out, one palm up, the other down. "No, the other way," said the psychiatrist. So Feynman reversed both hands, leaving one palm down and the other up.
Feynman wasn't merely playing mind games; he was indulging in a little group-theoretic humor. If we consider all the possible ways he could have held out his hands, along with the various transitions among them, the arrows form the same pattern as the mattress group!
- They may also be labelled, and weighted, as in
Strogatz's article on "The Enemy of My Enemy":

"The enemy of my enemy is my friend." -- 'The corners signify people, companies or countries, and the sides connecting them signify their relationships, which can be positive (friendly, shown here as solid lines) or negative (hostile, shown as dashed lines).'

'Social scientists refer to triangles like the one on the left, with all positive, sides balanced, -- there's no reason for anyone to change how they feel, since it's reasonable to like your friend's friends. Similarly, the triangle on the right, with two negatives and a positive, is considered balanced because it causes no dissonance; even though it allows for hostility, nothing cements a friendship like hating the same person.'
'Leaving aside the verisimilitude of the model, there are interesting questions here of a purely mathematical flavor. For example, in a close-knit network where everyone knows everyone, what's the most stable state? One possibility is a nirvana of goodwill, where all relationships are positive and all triangles are balanced. But surprisingly, there are other states that are equally stable. These are states of intractable conflict, with the network split into two hostile factions. All members of a given faction are friendly with one another, but antagonistic toward everybody in the other faction. (Sound familiar?) Perhaps even more surprisingly, these polarized states are the only states as stable as nirvana. In particular, no three-party split can have all its triangles balanced.'
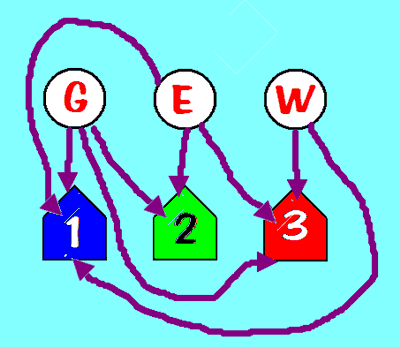
- Exercise: Let's draw all the simple graphs with three vertices.
- A cycle is a route from a node back to itself that doesn't retrace steps.
- One of these graphs is a tree: a graph that has no cycles.
- Where have we seen trees used before?
- Duality -- again!
- Exercise: How about all
the simple graphs with four vertices. (These are different from the
Facebooks, because there we distinguished vertices -- here we use
symmetry, treating all vertices as the same.)
- Have you ever seen any of these before? Could we give any of them names?
- Finally I just want to show you all
the simple graphs with five vertices. I'm really proud of this creation, which is as close to art as I come! :)
- Planar graphs are graphs that can be drawn such that no two edges
intersect. Every Platonic
graph can be drawn this way, so they are planar graphs.
- Complete graphs are simply graphs with connections between
every pair of vertices (but no loops).
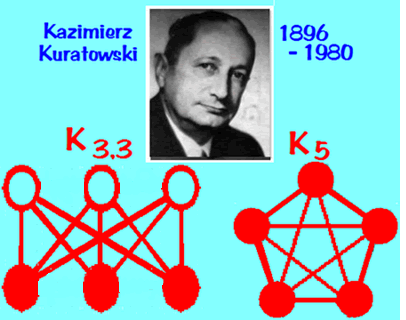
- Exercise: Let's see if we can show that the complete graph
with five vertices is not planar: