Day 57 in MAT229

• We're in our final week! Week 16.

• Our last week wraps up your intro to vectors, with an eye towards how we can use these moving forward.

• No new weekly assignment (although there will be IMath assignments)

• Exam 4:
  • The exam
  • A key
  • Grades:
    • Average grade (%): 80
    • Median grade (%): 80
    • Standard deviation (%): 10.53
    • Min grade: 56.25%
    • Max grade: 96.25%

• Details on the final exam are in:
  • We're going to hold it at the time slot for the TR classes starting at 1:40, which is Thursday, 5/6, 12:20-2:20.

  • We are open to allowing those who would prefer taking it in the TR at 9:25 slot (which is Tuesday, 5/4, 10:10-12:10) to do so. Let me know if this is you.

  • You will be allowed a page of notes and a calculator.

One (the dot product) is a scalar product (produces a number), while the other (the cross product) is a vector product -- producing a vector.

• Last week:

  In the lab I talked about establishing a "local coordinate system" for motion (called the "Frenet Frame" -- you should really watch this video until 5:15, at least!).

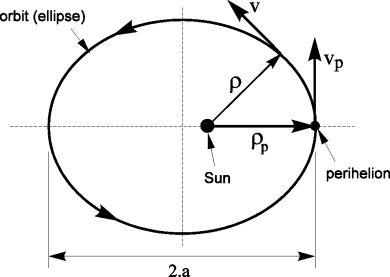
  Inspection of this figure will illustrate an important feature of planetary motion: Kepler's second law, which illustrates that a body in orbit about the sun will sweep out equal areas in equal times:

  

  Furthermore this illustrates other important things: time-varying vectors, representing position relative to the sun and velocity of a planet in orbit about the sun; perpendicularity (notice the third vector, which is neither the tangent vector, nor the vector "connecting" the planet to the sun (which is at the origin of the coordinate system). That vector is part of the Frenet frame -- a localized coordinate system on the rotating planet.

  It also illustrates the calculation of an area in polar coordinates.

  The Frenet frame includes another (third) direction, which will be perpendicular to the plane of the planet's motion. That vector extends out of the plane of motion. It is the cross-product that permits us to construct that vector.

• Materials:
  • Dot Products (.nb)
  • Dot Products (.pdf)
  • Long talks you through dot products.

• Equation of the cardiod: $r(\theta)=1-\cos(\theta)$
  

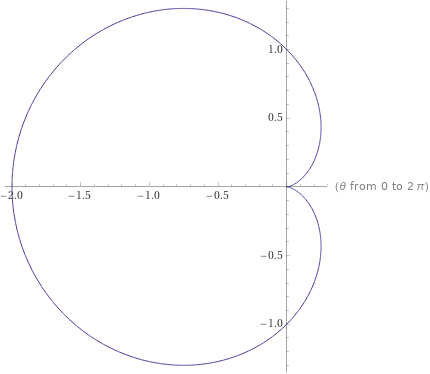
• Area of the cardiod: $A=\frac{1}{2}\int_{0}^{2\pi}(1-\cos(\theta))^2\ d\theta = \frac{3\pi}{2}\approx 4.71$

• Length of the cardiod: $L=\int_{0}^{2\pi}\sqrt{(1-\cos(\theta))^2+(\sin(\theta))^2}\ d\theta = 8$