- It's lab time, in our final week: Week 16.
- Zoom:
- Start it.
- Video on.
- Can everyone hear?
- Share screen.
- Record.
- Our last week wraps up your intro to vectors, with an eye towards
how we can use these moving forward.
- No new weekly assignment (although there will be IMath assignments)
- Because I don't like to make things due in finals week, anything
with a due date in that week is optional, and serves as a
replacement for lower grades.
I would do these labs, and IMath exercises anyway -- because they're preparing you for the final. But don't sweat the grades, because they can only help you. That being said, if you need the help, it's time to do them and do well on them....
- Details on the final exam are in:
- We're going to hold it at the time slot for the TR classes
starting at 1:40, which is Thursday, 5/6,
12:20-2:20.
- We are open to allowing those who would prefer taking it
in the TR at 9:25 slot (which is Tuesday, 5/4,
10:10-12:10) to do so. Let me know if this is you.
- You will be allowed a page of notes and a calculator.
- We're going to hold it at the time slot for the TR classes
starting at 1:40, which is Thursday, 5/6,
12:20-2:20.
- Before we begin, a tangent on tangents:

Does it appear that the tangent lines provide a meaningful prediction of future CO2 levels?
Using calculus terms, how would you characterize the growth in CO2 levels in the atmosphere?
-
The dot product (pdf summary) is one
of two vector products that we are considering this week. The cross
product (pdf summary) will be
featured in tomorrow's material.
The dot product ${\overline{u}}\cdot{\overline{v}}$ is a scalar product (produces a number). The number reflects the extent to which the two vectors ${\overline{u}}$ and ${\overline{v}}$ are aligned or not. In particular, the dot product is 0 when two vectors point in perpendicular directions. Thus it provides a test for perpendicularity.
It also is used to compute the length of a vector: \[ |{\overline{u}}|=\sqrt{{\overline{u}}\cdot{\overline{u}}} \]
Finally, the dot product provides a means for computing the angle $\theta$ formed between two vectors when their butt ends are located at the same point:
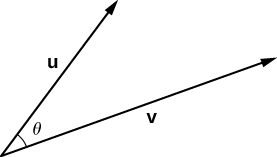
\[ {\overline{u}}\cdot{\overline{v}} = |{\overline{u}}||{\overline{v}}|\cos(\theta) \]
If we know the components of the vectors, e.g. ${\overline{u}}=\langle u_1,u_2,\ldots,u_n\rangle$ for the $n$-dimensional vector, then its easy to compute the dot product of two vectors: \[ {\overline{u}}\cdot{\overline{v}} = \sum_{i=1}^n u_i v_i \]
- Materials:
- lab 16 (.nb).
- lab 16 (.pdf).
- Zoom recording (Tuesday)
- Zoom recording (Thursday) -- sorry, this was recorded on the local computer, so no text to go along with....
- Another week and we'd have everything we need to understand
Kepler's First Law: that planets travel in elliptical paths around the
sun.