- It's hump day in Week
16.
- Details on the final exam are in:
- We're going to hold it at the time slot for the TR classes
starting at 1:40, which is Thursday, 5/6,
12:20-2:20. It will be held on Canvas, but you will
have two hours to do it.
- We are open to allowing those who would prefer taking it
in the TR at 9:25 slot (which is Tuesday, 5/4,
10:10-12:10) to do so. Let me know if this is you.
- You will be allowed a page of notes and a calculator.
- We're going to hold it at the time slot for the TR classes
starting at 1:40, which is Thursday, 5/6,
12:20-2:20. It will be held on Canvas, but you will
have two hours to do it.
-
The dot product (pdf summary) is one
of two vector products that we are considering this week, which we
considered on Monday. The cross product (pdf summary) is featured today.
The cross product ${\overline{u}}\times{\overline{v}}$ is a vector product (produces a vector) -- but only works in three-dimensions. Its magnitude reflects the extent to which the two vectors ${\overline{u}}$ and ${\overline{v}}$ are parallel. In particular, the cross product has 0 length when two vectors point in parallel directions. Thus it provides a test for parallelness.
It also is used to compute the area of a parallelogram formed by putting the butts of the two vectors together: \[ |{\overline{u}}\times{\overline{v}}|=|{\overline{u}}||{\overline{v}}| \sin(\theta) \] Notice that the parallelogram has zero area when the vectors are parallel, and maximal area when the vectors are perpendicular.
Finally, the cross product provides a means for producing a vector perpendicular to both ${\overline{u}}$ and ${\overline{v}}$ -- so enables us to "leap from a plane", as it were, the plane in which that parallelogram, formed by putting the butts of the two vectors together, lives.
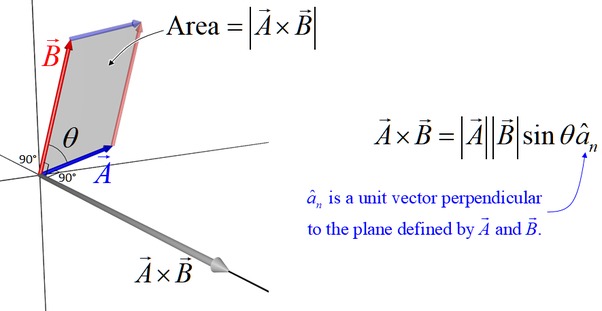
Since I borrowed this image I shouldn't be too critical, but it's important to note that the unit vector mentioned, $\hat{a}_n$, is the unit vector chosen by the right-hand rule (more about that in the materials below). I believe that the use of the subscript "$n$" on that unit vector indicates "normal" -- that is, perpendicular -- to the plane.
- Materials:
- Cross Products (.nb)
- Cross Products (.pdf)
- Long talks you through cross products.
- Another week and we'd have everything we need to understand
Kepler's First Law: that planets travel in elliptical paths around the
sun.