- Your third and final midterm exam is this weekend, starting today
(Friday). It covers sections 4.1, 6.1-6.3, and 7.2-7.4. That's
a bunch of sections. Coverage will be even however, so expect
about one problem from each section (although I may be able to
combine a few sections into a single problem).
- The exam will open at 5:00 pm, Friday, and close at 9:00 pm Sunday.
- You may have one page of notes.
- As usual, it will be taken with the lockdown browser.
- Today I have a brief review, of key topics. I didn't hear anything
from anyone about special problems or issues to cover in this
review, so I trust that you're all ready.
- I've already posted my "Exam 2s" from the past -- those would
cover most of this material. You can check those out for some
sample problems (see day 15).
- Your Section 7.3 homework is graded (#11, 22, 28):
- This first problem was Bellman-Ford: so we're to find the
shortest distance from a given start node to every other
node (of which there are $n$ total). The strategy is similar to
Dijkstra's, except that we iterate by path length; so our first
"distance vector" is just the adjacencies of the start node,
then we add in "shortcuts" that use more and more nodes, until
we either reach paths of length $n-1$, or the vector of
distances doesn't change from one step to the next (in which
case it won't change again).
For comparison purposes, I also give the solution for exercise #1, which is Dijkstra's on the same graph. I illustrate the method using recursively smaller graphs, as described in the "lecture".
- We were to illustrate Kruskal's method for the construction of the minimal spanning tree. Make sure that you can illustrate that you're actually using the method. Can you distinguish between Prim's algorithm and Kruskal's?
- In this problem, the point was that by introducing a new
node you could cut the weight of the minimal spanning tree. So
you may want to do so, in a particular problem.
Many of you missed the idea behind this problem.
- This first problem was Bellman-Ford: so we're to find the
shortest distance from a given start node to every other
node (of which there are $n$ total). The strategy is similar to
Dijkstra's, except that we iterate by path length; so our first
"distance vector" is just the adjacencies of the start node,
then we add in "shortcuts" that use more and more nodes, until
we either reach paths of length $n-1$, or the vector of
distances doesn't change from one step to the next (in which
case it won't change again).
- Your Section 7.4 homework is graded (#2, 20, 36):
- Both of our graph traversal methods (depth-first and
breadth-first) are effectively building a spanning
tree. They just do it in two different ways.
I like the depth-first approach, because of its lovely recursive nature.
- However, I kind of prefer the breadth-first
traversal -- it takes care of the starting
node and all of its adjacencies ("children");
then asks its "first child" to do the same; if
after all that, the first child's "family tree" comes
up against a brick wall, we head back up the recursion
and move to the root's second child, etc.
- This is an interesting problem. I drew a diagram, which
may help to explain the situation.
Don't forget that the two sets of nodes may not have the same cardinality, and hence once set may run out first. What happens then?
- Both of our graph traversal methods (depth-first and
breadth-first) are effectively building a spanning
tree. They just do it in two different ways.
- I received the following from Prof. Newell, who asked me to
advertise his CSC485 course for this summer:
************************* I just wanted to point out to all of you that CSC-485/585 will be offered this summer session. This is the "Theory of Computation" course which is required for the Computer Science major. Theory can be a difficult course for some students and being able to focus upon that one course alone can be a great advantage for many. I have designed an online version of the course which has worked out quite well over the past 2.5 semesters (I know it sounds like I am bragging but it really is a good online course I think). The summer schedule is available and registration is open so if you are interested please sign up. If you are curious about what the course covers I can summarize it as follows: We search for the answer to one simple question : "What is computable?" or, to put it another way, "Are there problems that we cannot solve with any computer?". That is, we search for a simple model of computation which is equivalent in computational power to your friendly neighborhood computer and we try to determine if there are problems that cannot be solved using said model (Spoiler alert - there are!!!). We then find a way to actually prove that some problems are, in fact, unsolvable with ANY computational device - and I do not mean weird metaphysical questions like "What is the meaning of life?" or "Can God create a stone that she herself can't lift?" or stuff like that - I mean clear problems that can be stated in straight-forward mathematical terms. Along the way, as we search for our model and proof technique, we discover models for other families of problems that are quite useful in day to day problem solving and we discover properties about them which we can use in our repertoire of programming skills. If you have any questions, please let me know. Also, please keep in mind that, as a required course, CSC 485 often fills up very quickly during the Fall/Spring semesters. If you have any questions about the course or anything else that I can help you with feel free to contact me at newellg@nku.edu *****************************
- I didn't create a video for this. I'll just present the highlights.
Chapter 7 material was covered on Day 22, although summaries are also included here. So let's step through the rest of the material to be covered on this exam: sections 4.1, and 6.1-6.3.
- Details of examples of Dijkstra's, Bellman-Ford, and Floyd's algorithms (including homework problems from 7.3)
- Depth first and Breadth first algorithms for problems from Gersting (in lisp)
- Dijkstra's algorithm, pruning the original graph.
Copy and paste this adjacency graph to reproduce the results of the animated gif from Wikipedia:
0 7 9 nil nil 14 7 0 10 15 nil nil 9 10 0 11 nil 2 nil 15 11 0 6 nil nil nil nil 6 0 9 14 nil 2 nil 9 0
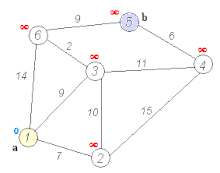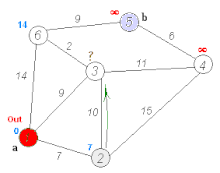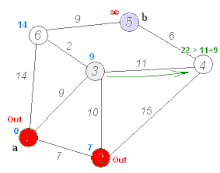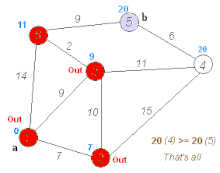
- Here's a traversal which was a student's idea, based on the breadth-first algorithm. It computes the distances between all pairs of vertices (like Floyd's algorithm).