-
- This session will be captured on Zoom, if I remember to turn it on, and record it.
- Our page of zooms and the play-by-plays.
- You have a symmetry assignment due today.
- Important: a student panicked because he saw that the
weights on the review IMath exercise were much higher than the
other IMath exercises. Each homework is equally weighted: what
matters is your percentage grade on each.
I will drop a couple of your lowest homework scores.
- The second exam is returned.
- I happened to notice that the logo for NKU's CINSAM (Center for
Integrative Sciences and Mathematics) should be familiar, which brings
us to logos!
You want to start thinking about your Mathematical logo. We have a couple of "logo-popular" topics left (e.g. fractals, knots, infinity); but you may have already seen something that inspires you (some people like spirals -- like CINSAM!).
At any rate, you want to start thinking about this. Two of our final days will be dedicated to presenting our logos in class (or on-line for the on-line section).
In-person presentations include a one-page, type-written description of your logo -- what it is (specifically, mathematically -- what are its mathematical elements?), why you chose to use the components you did.
- Symmetric objects in three-dimensions: Platonic solids, which possess a great deal of symmetry: they're super-symmetric solids.
- These are the analogs of the regular polygons
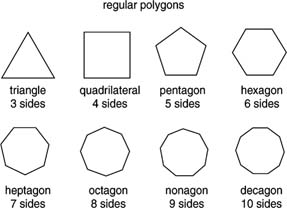
But, in contrast to the regular polygons (of which there are infinitely many), there are only five!
The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia! Tetrahedron Hexahedron
or CubeOctahedron Icosahedron Dodecahedron 




fire earth air water universe - We learned that they have twins -- duals -- that share certain
properties.
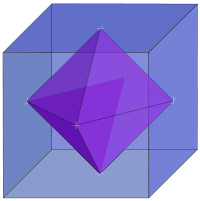
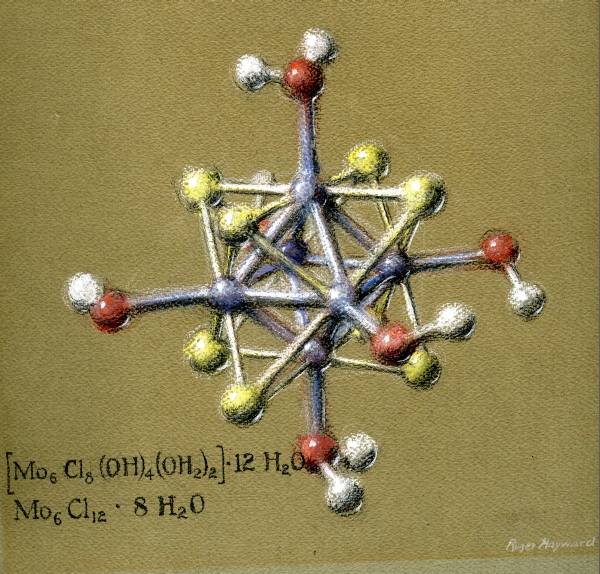
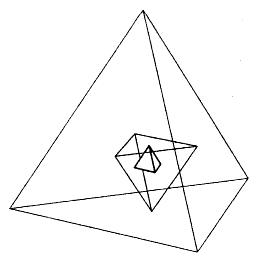
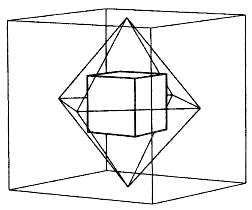
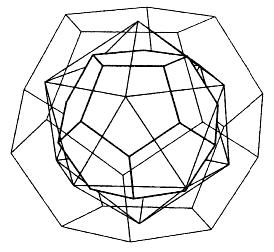
But one of the coolest things is that they fit within each other like "Russian dolls". And nature knows it, as shown in the compound of Molybdenum Dichloride molecules shown here.
- We'll be doing some "playing" today, with some kits which I
discovered long ago -- but which are perfect for getting your hands on
these Platonic solids.
I'll turn you loose in a bit, to build your own magnetically beautifully solids, but, before we go, I want to remind you of a couple of ideas -- one in particular which points to our future (fractals):
- We talked about duality, and that each solid has a partner: here they are together.
I hope that this has you imagining "Russian Dolls", which are those which stack in such a way that there is a perfect copy of a doll inside each doll, only smaller (self-similarity at a smaller scale):

- How can we draw the Platonic solids on a sheet of paper? We
project them onto the paper, turning them into planar
graphs:
- The tetrahedron can be drawn to be a "distorted" Mercedes symbol, as we've seen.
- The cube you've undoubtedly done before.
- The others are more complicated, but here are all the solids:
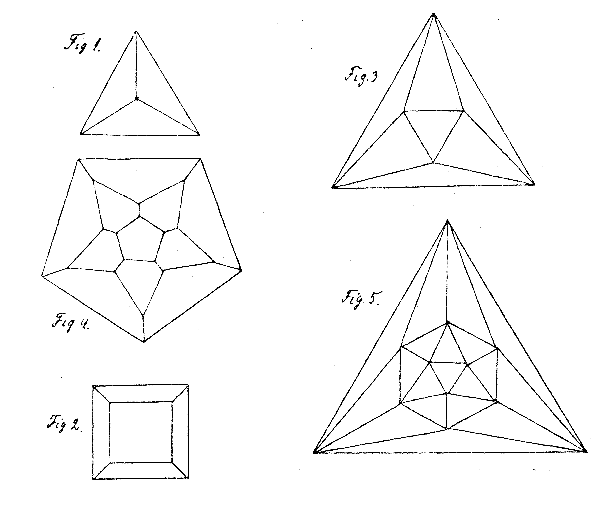
Practice drawing them! Color them and make them pretty....
Can you see the duality?
- The graphs may help you to complete this table about these solids:
# of Vertices # of Edges # of Faces faces at each vertex sides on each face Tetrahedron 4 6 4 3 3 Cube Octahedron Dodecahedron Icosahedron What conclusions can we draw from this data? Is there a pattern? (Of course there is!:) The pattern leads to the concept of "Duality".
We can also verify that the Platonic solids satisfy Euler's formula, even though they're three dimensional objects! Their graphs are planar, however, as you can see!
- Symmetry, by Hermann Weyl (Princeton University Press, 1952)
- Symmetry of lifeforms on Earth
- A fun reading on symmetry
- Fibonacci
Spiral Fractal maker.
- How to win at Nim
- Unit Fraction Table
- How Egyptians wrote fractions.
- Problem 81: converting between different measures with fractions
- Egyptian fractions (Wikipedia)
- An amazing source for Egyptian Fraction info
- The new Mayan glyphs from Xultun, Guatemala: lots of spectacular calendar calculations, but nothing whatsoever about 2012 AD
- "Ancient Maya Astronomical Tables from Xultun, Guatemala". William A. Saturno, David Stuart, Anthony F. Aveni, Franco Rossi
- Part of the wall from which our Mayan tablet is taken