- This session will be captured on Zoom, if
I remember to turn it on, and record it. Please help me to remember.
Here's a menu of our past zooms...
I'll post the link to today's later. These zooms will continue through February 7th, for those who can't attend in person.
- For today, you were to read Section 1.2 in
our text, and carry out Preview Activity 1.2.1.
I asked you to bring the Preview Activity and the Completed worksheet to class, to submit for my perusal. I just want to get a look at your work.
- For next time: Let's keep rolling: read Section
1.3: The derivative of a function at a point, and carry out the
preview exercise (I won't ask you to hand this one in; but
bring your work to class, because it will be graded "informally".).
Also carry out the following two exercises (due next Monday, at 2:00 pm (before class), to submit on Canvas): Section 1.1, #8; Section 1.2, #7.
- Roll
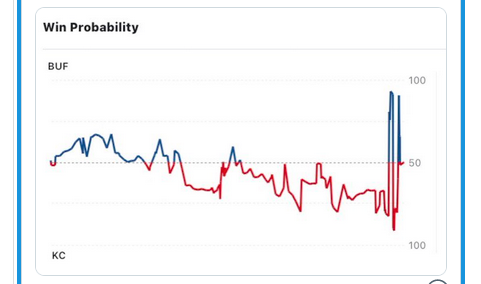
- Chiefs v Bills: did we just witness the greatest two minutes in
NFL history?
"In the two-minute span, there were three lead changes and a tie. Twenty-five points scored. The quarterbacks combined for 221 passing yards and three touchdowns in the same period."
And how is all of this illustrated in the "win probability chart"?
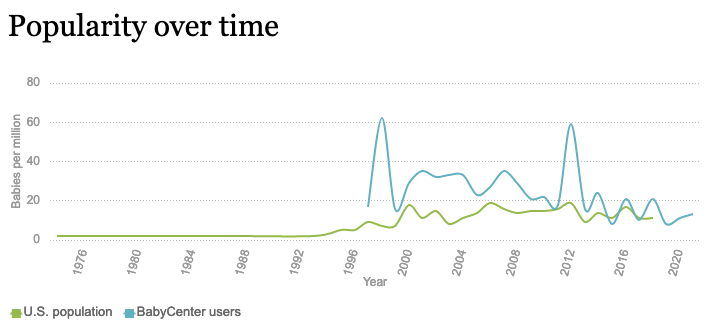
- Here is the popularity graph for the name "Saffron". Tell me a story!
- The key concept is average velocity; the interesting notion is instantaneous velocity!
The key to that "instantaneous" velocity is something called an "indeterminate form", and limits. We'll get a look at that in the activity we do next, but it's hinted at by thinking about average velocity: as we noted last time, it's a change in $y$ over a change in $x$:
\[ AV = \frac{\textrm{change in y}}{\textrm{change in x}} \]
Now what happens as that "change in $x$" approaches 0? (that's the "limit" part!)
If all is well in the world, then the ratio becomes indeterminate because the "change in $y$" also approaches 0! And everyone knows what $\frac{0}{0}$ is, right? (that's the "indeterminate" part!)
-
Key ideas are limits, from the left and from the
right, and then a definition of instantaneous
velocity. There's an important definition of limit in
this section, as well (Definition 1.2.2). Let's take a look at
that first.
\[ \begin{equation*} IV_{t=a} = \lim_{b \to a} AV_{[a,b]} = \lim_{b \to a} \frac{s(b)-s(a)}{b-a}\text{.} \end{equation*} \]
or, equivalently,
\[ \begin{equation*} IV_{t=a} = \lim_{h \to 0} AV_{[a,a+h]} = \lim_{h \to 0} \frac{s(a+h)-s(a)}{h}\text{.} \end{equation*} \]
- Let's see how this definition works in the case of that
function we looked at last time, and the instantaneous velocity
at the point $a=2$:
\[
s(t)=64-16(t-1)^2
\]
- One of the interesting ideas is that of a discontinuity
in a function: not all functions are smooth, or even connected!
What that means is that the definition above may not make sense
in some cases. What can go wrong? Three things:
We interpret the derivative as the slope of the tangent line (the limit of secant lines!) at a point. You can frequently look at a graph and see where things go awry. Take a look at the football graph above, and describe where problems exist. For example, if there's no tangent line at a point, then there's no instantaneous velocity!
- Because there are so many musicians in here, I
thought that we'd listen to the sound
of a function.... In particular, I want you to listen for
the "sounds of discontinuity".
- My freshman physics professor at Miami University, Prof. Don C. Kelly wrote The Little Book of Calculus. Self-Help Guide to Calculus. I just found this yesterday, on his website, and it's a neat "little" (50 some pages) resource produced by him and his kids/grandkids. Check out page 12, limits....