- Reminder that we're going to be in MEP314 from now on.
- We're going to jump ahead to chapter 2 next time. Please read section 2.1 to prepare, and do the preview exercise to submit on Canvas prior to our Monday meeting.
- Here's our whiteboard work for the day:
- Let's start in on your
Section 1.6 worksheet (second derivatives).
I had a couple of questions on it, and we really didn't make enough progress to justify submitting it before class. You can do that after class!
- Then we'll hit section 1.8: The Tangent Line Approximation
The upshot is that linear functions are good approximations to smooth functions (functions with derivatives), if you zoom in close enough.
-
An important first step was using what we call the
"linearization", the tangent line: we use the fact that
\[
f(a+h) \approx f(a) + hf'(a)
\]
This comes straight out of the limit definition, where we throw
away the limit. That's why we have to write "$\approx"$:
\[
f'(a) \approx \frac{f(a+h)-f(a)}{h}
\]
-
So if we define $x=a+h$, then
\[
f(x) \approx f(a) + f'(a)(x-a)
\]
or
\[
f(x) \approx y = f(a) + f'(a)(x-a)
\]
The tangent line serves as an impressive approximating machine, provided
$h=x-a$ is small enough. (How small is "small enough?")
We can see why this works well if we get "small enough", if we visit the website suggested by our authors.
-
That linear function given by the tangent line, $y = f(a) + f'(a)(x-a)$,
is called the local linearization of $f$ at the point $(a,f(a))$:
$L(x)=f'(a)(x-a)+f(a)$ - For example, suppose you need to compute $\sqrt{15.96}$. Now the
easy way is to use your calculator, but the cowboy way would be to use
the linearization! Let's have a go at that one.
- We know the square root of 16, which is close: our answer should be near 4.
- Draw a picture! The picture will demonstrate two different
types of quantities that we want to discuss:
differentials $dy$, and increments $\Delta y$.
Differentials versus increments
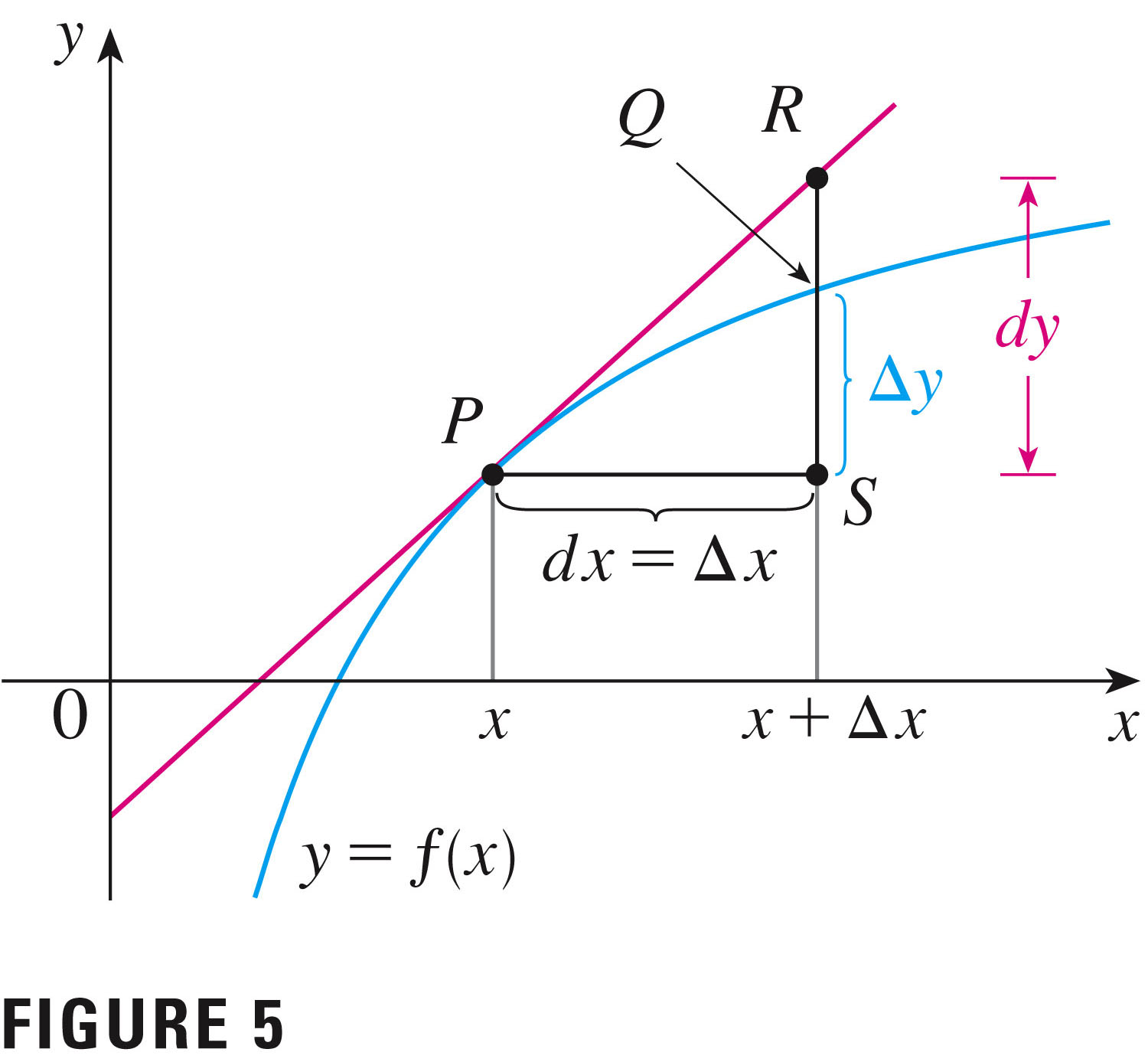
The increment is the true change in the function value; the differential approximates the true change: One way to remember the difference:- Differentials $dy$ follow the direction suggested by the derivative
- Increments $\Delta y$ are actual changes in the function value.
$dy \approx \Delta y$
We want the increment, but may settle for the easily computed differential.
- Compute the derivative of $f(x)=\sqrt{x}$ at $x=16$, and
we can write down the tangent line equation:
\[
L(x) = (x-16)/8 + 4
\]
- We use the tangent line for our approximation, and, when
we're done, we can ask "is our answer an over- or an under-estimate?"
The answer takes us back to the second derivative:
- We know the square root of 16, which is close: our answer should be near 4.
- For today's worksheet, we'll work some activities and homework problems from section 1.8.
- For example, suppose you need to compute $\sqrt{15.96}$. Now the
easy way is to use your calculator, but the cowboy way would be to use
the linearization! Let's have a go at that one.
-
An important first step was using what we call the
"linearization", the tangent line: we use the fact that
\[
f(a+h) \approx f(a) + hf'(a)
\]
This comes straight out of the limit definition, where we throw
away the limit. That's why we have to write "$\approx"$:
\[
f'(a) \approx \frac{f(a+h)-f(a)}{h}
\]
