- If you need to Zoom to class, here's the
link.
- Today we are going to use our primary tool, the limit definition
of the derivative, and build all kinds of new tools. Strap on your
seatbelts!
- You've got a new homework assignment:
- Read section 2.2 (derivatives of sines and cosines); do the preview and submit prior to class next time.
- You have a new IMath problem set.
- Here's our whiteboard work for the day:
- Last time we talked about using the tangent line function (which we call the
"linearization" of $f$ about $x=a$)
\[
L(x)=f'(a)(x-a)+f(a)
\]
- Let's review our example: suppose you need to compute $\sqrt{15.96}$. Now the
easy way is to use your calculator, but the cowboy way would be to use
the linearization! Let's have a go at that one.
- We know the square root of 16, which is close: our answer should be near 4.
- Draw a picture! The picture will demonstrate two different
types of quantities that we want to discuss:
differentials $dy$, and increments $\Delta y$.
Differentials versus increments
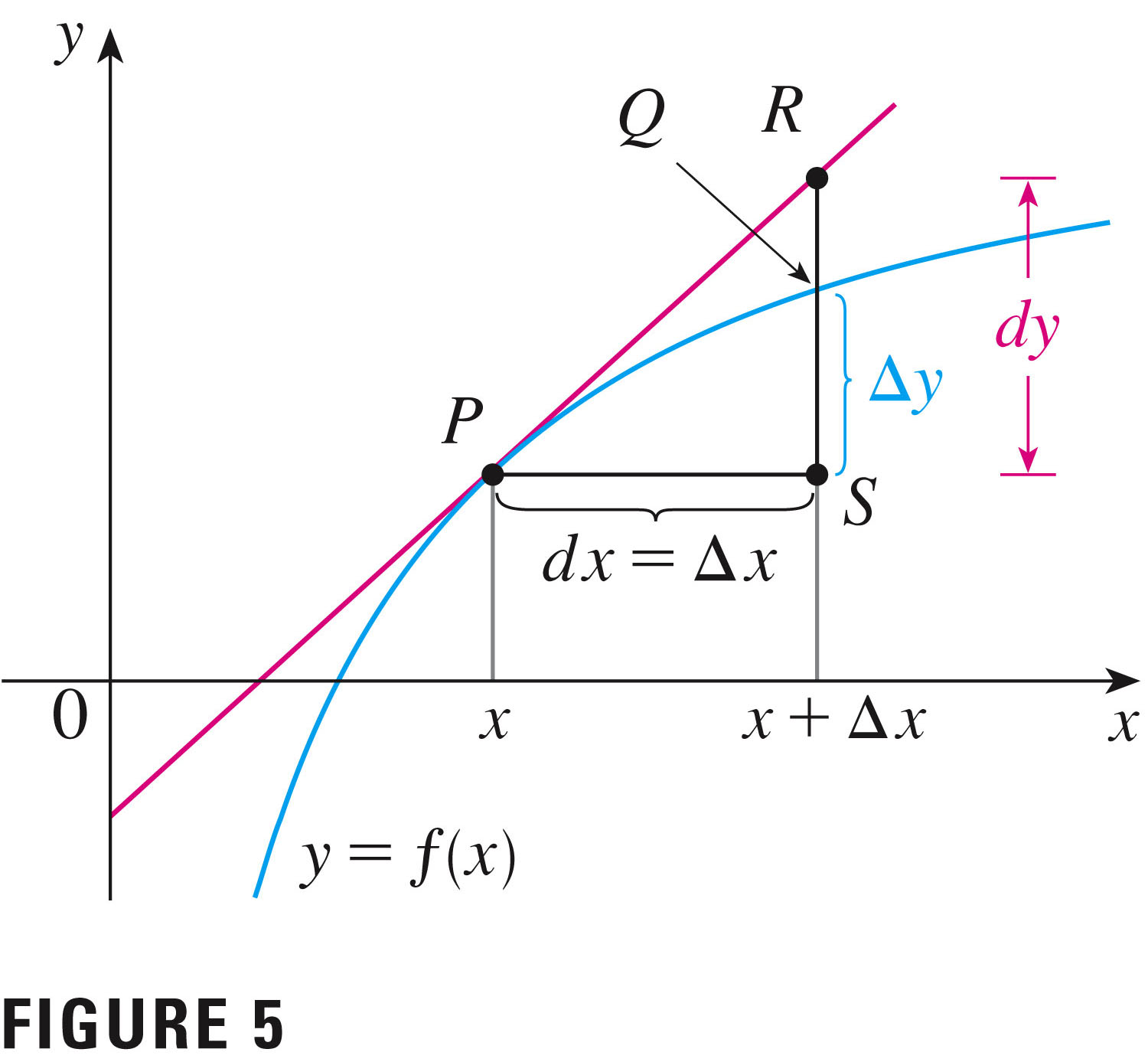
The increment is the true change in the function value; the differential approximates the true change: One way to remember the difference:- Differentials $dy$ follow the direction suggested by the derivative
- Increments $\Delta y$ are actual changes in the function value.
$dy \approx \Delta y$
We want the increment, but may settle for the easily computed differential.
- Compute the derivative of $f(x)=\sqrt{x}$ at $x=16$, and
we can write down the tangent line equation:
\[
L(x) = (x-16)/8 + 4
\]
- We use the tangent line for our approximation, and, when
we're done, we can ask "is our answer an over- or an under-estimate?"
The answer takes us back to the second derivative:
- We know the square root of 16, which is close: our answer should be near 4.
- Let's review our example: suppose you need to compute $\sqrt{15.96}$. Now the
easy way is to use your calculator, but the cowboy way would be to use
the linearization! Let's have a go at that one.
- Today I'm going to plow through a bunch of "proofs"; the objective
is to create a bunch of useful new tools out of our old (but
good) tool, the limit definition of the derivative:
\[
F'(x)=\lim_{h \rightarrow 0}\frac{F(x+h)-F(x)}{h}
\]
Here we go! For the following proofs, assume that functions $f$
and $g$ are differentiable at $x$.
- Theorem: Let $F(x)=c$ where $c$ is a constant. Then
$F'(x)=0$.
- Theorem: Let $F(x)=x$. Then $F'(x)=1$.
- Theorem (sum rule -- ``The derivative of a sum is the sum
of the derivatives.'' It rolls off the tongue....):
Let $F(x)=f(x)+g(x)$. \[ \frac{d}{dx}[F(x)] = \frac{d}{dx}[f(x)+g(x)] = \frac{d}{dx}f(x) + \frac{d}{dx}g(x) = f'(x) + g'(x) \] - Theorem (product rule -- not simply the product of
the derivatives!):
Let $F(x)=f(x)\cdot g(x)$. \[ \frac{d}{dx}[F(x)]=\frac{d}{dx}[f(x)\cdot g(x)]=f(x)\frac{d}{dx}g(x) + g(x)\frac{d}{dx}f(x) =f(x)g'(x) + g(x)f'(x) \] - Corollary (constant multiple rule): multiplying a
function by a constant scales it in the $y$ direction. This
makes it steeper by a factor of $c$.
Let $F(x)=cf(x)$. \[ \frac{d}{dx}[F(x)]=\frac{d}{dx}[cf(x)]=c\frac{d}{dx}f(x)=cf'(x) \] This is a consequence of the product rule (which is why we call it a corollary). - Theorem (Power rule):
Let $F(x)=x^n$, where $n$ is an integer greater than 1. \[ \frac{d}{dx}[F(x)]=\frac{d}{dx}(x^n)=nx^{n-1} \]This proof will also make use of one of our new tools (the product rule). Once you build and prove a tool, it becomes a power tool:).
The power works for any real exponent -- it's just that we've only proven it for positive integers. You may use it for other powers (e.g. $\sqrt{x}=x^\frac{1}{2}$).
- Theorem (quotient rule -- not simply the quotient of
the derivatives!):
Let $F(x)=\frac{f(x)}{g(x)}$. \[ \frac{d}{dx}[F(x)]=\frac{d}{dx}\left[\frac{f(x)}{g(x)}\right] = \frac{\frac{d}{dx}f(x)g(x) - f(x)\frac{d}{dx}g(x)} {[g(x)]^2} = \frac{f'(x)g(x) - f(x)g'(x)} {[g(x)]^2} \] I got a rhyme from a colleague, to help us remember this formula: ``Lo dee hi minus hi dee lo, over the denominator square they go!''.
Next time we'll add rules for derivatives of the trigonometric functions, and the exponential functions.But, at the moment, we've got all the power we need to differentiate (easily) any polynomial, and any rational function -- and that's a huge group of functions!
- Theorem: Let $F(x)=c$ where $c$ is a constant. Then
$F'(x)=0$.
- For today's worksheet, we'll work with polynomials and powers (negative, and other than simple integers): Sections 2.1 and 2.3 worksheet.
