- If you need to Zoom to class, here's the
link.
- Today we continue to use our primary tool, the limit
definition of the derivative, to build more new tools. Check
your seatbelt!
- You've got a new homework assignment:
- Read section 2.2 (derivatives of sines and cosines); do the preview and submit prior to class next time.
- Reminder that you have an IMath problem set on the go....
- Recent whiteboard work:
- Overall, your limit definition work looked REALLY GOOD. Keep it
up!
- The limit is an operator: that is $\displaystyle \lim_{h\rightarrow 0}$
doesn't make sense; only $\displaystyle \lim_{h\rightarrow 0}()$ makes sense.
The operator has to act on something (or, as I like to say, it needs something to eat!:).
What's $\sqrt{}$? (It's nothing without an argument.) What's $\sin{}$? (That's right -- sine without an argument is a sin!)
Treat limits the same way.
- So don't say
\[
\lim_{h\rightarrow 0}2x+h
\]
if you mean
\[
\lim_{h\rightarrow 0}(2x+h)
\]
The limit eats the whole thing; not just the 2x term (which is what the
first one says).
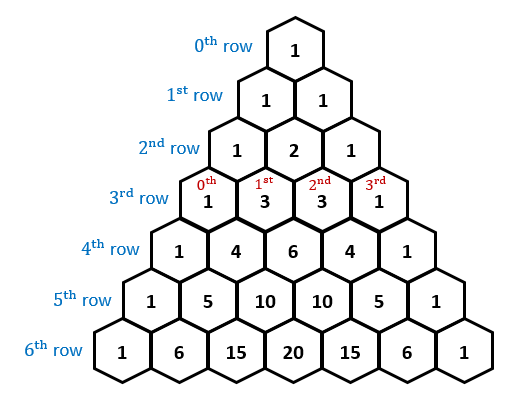
- Those coefficents they "give you" in the preview are available
free of charge from Pascal's triangle -- the coolest most powerful
little tool I know (after the limit definition of the derivative, of
course):
- Theorem: Let $F(x)=c$ where $c$ is a constant. Then $F'(x)=0$.
- Theorem: Let $F(x)=x$. Then $F'(x)=1$.
- Theorem (sum rule -- ``The derivative of a sum is the sum
of the derivatives.'' It rolls off the tongue....):
Let $F(x)=f(x)+g(x)$. \[ \frac{d}{dx}[F(x)] = \frac{d}{dx}[f(x)+g(x)] = \frac{d}{dx}f(x) + \frac{d}{dx}g(x) = f'(x) + g'(x) \] - Theorem (product rule -- not simply the product of
the derivatives!):
Let $F(x)=f(x)\cdot g(x)$. \[ \frac{d}{dx}[F(x)]=\frac{d}{dx}[f(x)\cdot g(x)]=f(x)\frac{d}{dx}g(x) + g(x)\frac{d}{dx}f(x) =f(x)g'(x) + g(x)f'(x) \] - Corollary (constant multiple rule): multiplying a
function by a constant scales it in the $y$ direction. This
makes it steeper by a factor of $c$.
Let $F(x)=cf(x)$. \[ \frac{d}{dx}[F(x)]=\frac{d}{dx}[cf(x)]=c\frac{d}{dx}f(x)=cf'(x) \] This is a consequence of the product rule (which is why we call it a corollary). - Theorem (Power rule):
Let $F(x)=x^n$, where $n$ is an integer greater than 1. \[ \frac{d}{dx}[F(x)]=\frac{d}{dx}(x^n)=nx^{n-1} \]This proof made use of one of our new tools (the product rule). Once you build and prove a tool, it becomes a power tool:).
The power rule works for any real exponent -- it's just that we've only proven it for positive integers. You may use it for other powers (e.g. $\sqrt{x}=x^\frac{1}{2}$).
- Today we plow through more "proofs", creating even more useful new
tools out of our old (but good) tool, the limit definition of
the derivative (plus the new rules we just built!):
\[
F'(x)=\lim_{h \rightarrow 0}\frac{F(x+h)-F(x)}{h}
\]
Again, for the following proofs, assume that functions $f$
and $g$ are differentiable at $x$.
- Theorem (quotient rule -- not simply the quotient of
the derivatives!):
Let $F(x)=\frac{f(x)}{g(x)}$. \[ \frac{d}{dx}[F(x)]=\frac{d}{dx}\left[\frac{f(x)}{g(x)}\right] = \frac{\frac{d}{dx}f(x)g(x) - f(x)\frac{d}{dx}g(x)} {[g(x)]^2} = \frac{f'(x)g(x) - f(x)g'(x)} {[g(x)]^2} \] I got a rhyme from a colleague, to help us remember this formula: ``Lo dee hi minus hi dee lo, over the denominator square they go!''.But we'll obtain this theorem by using tools we've already built; in particular, the product rule, and a trick to get the derivative of the multiplicative inverse of a function.
A theorem that you prove on the way to proving some theorem is called a "lemma".
- Lemma (derivative of the multiplicative inverse):
Let $F(x)=\frac{1}{g(x)}$. Then \[ \frac{d}{dx}[F(x)] = \frac{-g'(x)}{g(x)^2} \]
- Lemma (derivative of the multiplicative inverse):
- Theorem (exponential rule):
Let $F(x)=e^x$. \[ \frac{d}{dx}[F(x)] = F(x) \hspace{1in} (= F'(x) = F''(x) = F'''(x) = ....) \]where $e \approx 2.71828$ (it's irrational, like $\pi$).
This is certainly one of the most amazing rules. It says that $e^x$ is an exponential function which is its own derivative: whose values are its slopes, as well (and all its higher derivatives as well -- its concavity, its jerk, ...).
Here's an animation which motivates the discussion...
- Theorem (trigonometric derivatives):
Let $F(x)=\sin(x)$. \[ \frac{d}{dx}[F(x)]=\cos(x) \]We'll need a couple of limits to establish this one, as well as one trig identity: \[ \sin(a+b)=\sin(a)\cos(b)+\sin(b)\cos(a) \]
- Corollary:
Let $F(x)=\cos(x)$. \[ \frac{d}{dx}[F(x)]=-\sin(x) \]This is a consequence of the derivative of sine, by symmetry and periodicity.
Further consequences: \[ \frac{d^2}{dx^2}[\sin(x)]=-\sin(x) \] \[ \frac{d^3}{dx^3}[\sin(x)]=-\cos(x) \] \[ \frac{d^4}{dx^4}[\sin(x)]=\sin(x) \]
The sine (and cosine) functions are their own fourth derivatives.
- Theorem (quotient rule -- not simply the quotient of
the derivatives!):
- For today's worksheet, we'll work with a wide variety of functions, but there is a special focus on the exponential functions: Chapter 2 worksheet.
- The source of the animation of the exponential functions. Thanks to conroy....