Day 4, Mat128: Calculus A

Any questions on those? We'll look over the solutions next time.

Your "preview" for Wednesday is to "Explore" two of the "GeoGebra" examples mentioned in this section (there are questions at the end of each); these are the work of Marc Renault, at Shippensburg University:

1. One-sided limits
2. The Derivative at a Point

1. Something of a key
2. Secant lines -- passing through two points (which we can determine from the formula for \(h(t)\) at the two times)
3. Average velocity (slope of the secant line) -- instantaneous velocity is the slope of the "tangent line": the line which just kisses the curve at a point.

   Connections: Since we can see the secant line, and that its slope is negative, we know that the average velocity must be negative, too!

4. We need to know point-slope and slope-intercept forms of lines: \[ y-y_1 = m(x - x_1) \] \[ y = mx + (y_1 - m x_1) \equiv mx + b \] Notice that we must have independent and dependent variables in each (in this general case, \((x,y)\), but in the specific case here we might have used \((t,h)\)).

This figure presents us with the basic idea:

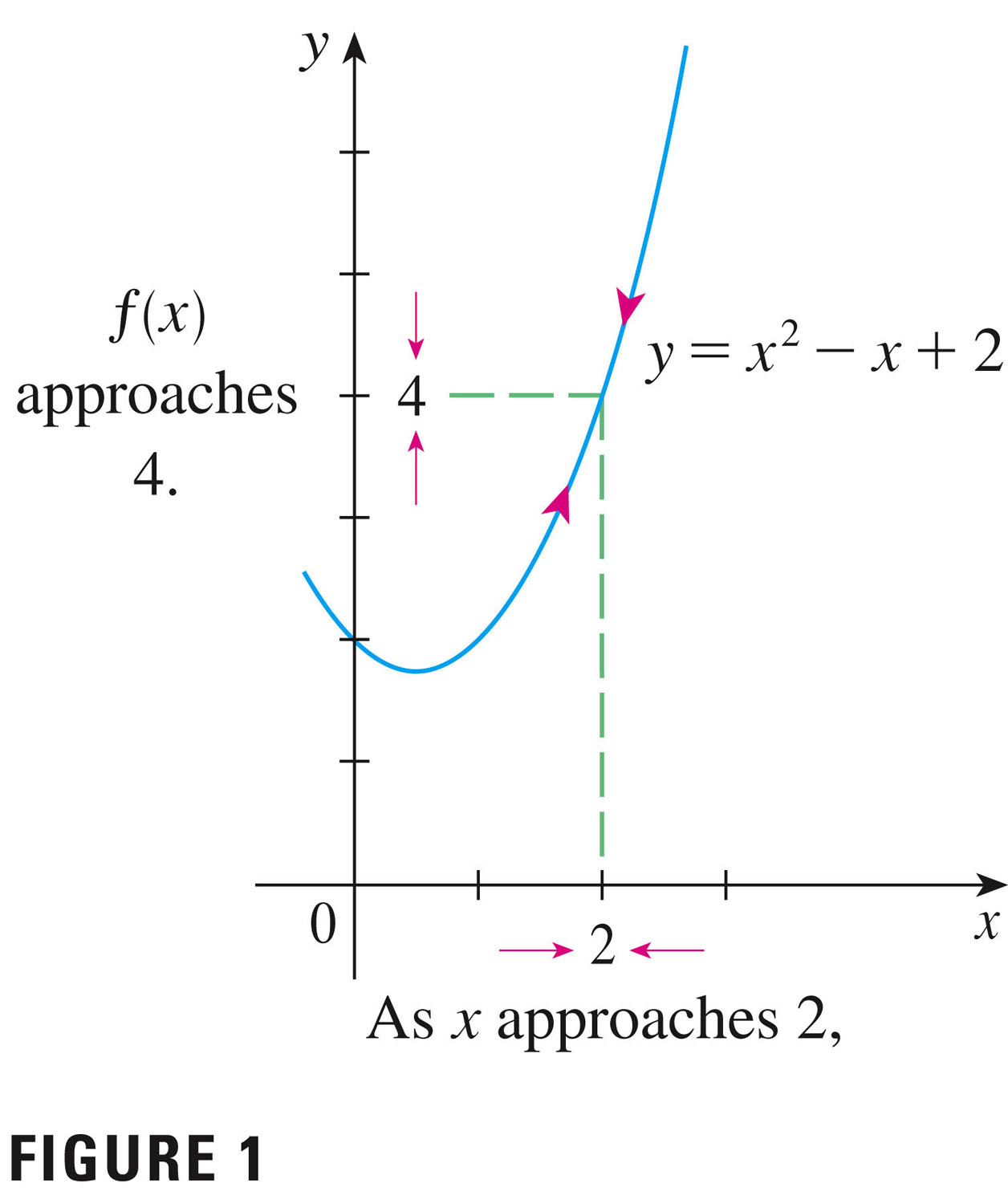
So we would say that

\[ \lim_{x \to 2}f(x)=4 \]

limit of $f(x)$ as $x$ approaches $a$: Suppose function $f(x)$ is defined when $x$ is near the number $a$ (this means that $f$ is defined on some open interval that contains $a$, except possibly at $a$ itself.) Then we write \[ \lim_{x \to a}f(x) = L \] if we can make the values of $f(x)$ arbitrarily close to $L$ by taking $x$ to be sufficiently close to $a$ but not equal to $a$. We say that ``the limit of $f(x)$ as $x$ approaches $a$ equals $L$.'' The intuitive idea is that in the neighborhood of $a$, the function $f$ takes on values close to $L$, and those values get closer the closer we get to \(a\).

Questions:

• In the figure above ("FIGURE 1"), what is $a$, and what is $L$?
• To what class of functions does $f$ belong?
• Do limits care about what happens exactly at $a$?

We can approach $x=a$ from the left or from the right. We define limits from the left and from the right, and then say that the limit exists as $x$ approaches $a$ if and only if the limits from the left and right exist, and agree: if the limit as $x$ approaches $a$ from the left, \[ \lim_{x \to a^-}f(x) = L \] and the limit as $x$ approaches $a$ from the right, \[ \lim_{x \to a^+}f(x) = L \] then the limit as $x$ approaches $a$ exists, and \[ \lim_{x \to a}f(x) = L. \]

The graphs of all functions are not necessarily smooth, or even connected!

The best case scenario is when the limit exists at a point, the function exists at that point, and the limit is the same as the function value: \[ \lim_{x \to a}f(x) = f(a). \] If that is the case, we say that \(f\) is continuous at \(a\).

This graph shows us that the function \(g\) is continuous at \(x=-1\):

\[ \lim_{x \to -1}g(x)=3=g(-1) \]

But this graph also illustrates that there are three things that can go wrong:

1. The function may not exist at a point
2. The limit may not exist at a point
3. The two may exist but not agree.

Why is continuity in a graph important? We interpret the derivative as the slope of the tangent line (the limit of secant lines!) at a point. You can frequently look at a graph and see where things go awry. For example, if there's no tangent line at a point, then there's no instantaneous velocity! And at any point of discontinuity, it's impossible to create a tangent line (so there's no derivative).

This should look familiar because we did something similar last class, in the case of the function \[ f(x)=9-x^2 \] a preview of a preview!:)

The most important definition in calculus is the definition of the derivative (here is the derivative of $f$ at $a$):

\[ f'(a)=\lim_{h\to 0}{\frac{f(a+h)-f(a)}{h}} \]

We've seen this in another form as well:

This was defined as the slope of the tangent line to a curve (provided the tangent line exists).

• Function representation -- tables, graphs, algebraic expressions
• Variables -- independent and dependent. [In the first limit above, the independent variable is actually $h$ for a fixed value of $x$: \(x=a\).]
• Domains and Ranges
• Function composition (remember this in the case of "frequency modulation" of a sine wave in our "sound functions".
• Ratios!
• Indeterminate things... (division by 0)

  In particular, we're only going to have indeterminacy in our derivative if the numerator goes to 0 when the denominator goes to 0. But that only happens if \[ \lim_{h\to 0}(f(a+h)-f(a))=0 \] This happens when the limit exists, and is equal to the function value. This is equivalent to \[ \lim_{h\to 0}f(a+h)=f(a) \] In order for this to be true, it must be the case that $f$ is continuous at $x=a$.

  We see, therefore, that a derivative exists at $a$ only if the function is continuous there. But not vice versa. A function continuous everywhere does not necessarily have a derivative everywhere -- can you think of one?

We've already seen how the secant lines approach the tangent line for a smooth curve. It's one of the first important problems we'll want to address in calculus. It's why we're interested in limits of things at the outset.

We usually find the equation of a line using two points, or a point and a slope. The secant line method approaches the tangent line at a point by using a succession of nearby points that are ever closer to the point of tangency: see, for example, this code suggested by our authors, the work of David Austin of Grand Valley State University:

The secant line method approaching the tangent line

The tangent ("touching") line osculates ("kisses") the curve at this point.

Notice the focus on linear functions: linear functions are the most important functions in calculus.

Once we have the derivative at $x=a$, we can write the equation of the tangent line, graph of linear function $y=T(x)$, using "point-slope" form: \[ y - f(a) = f'(a)(x-a), \] or \[ y = f'(a)(x-a) + f(a). \] It's that simple!

• Limits may be infinite (one-sided, perhaps). Here's how we define that:

  infinite limits for $\displaystyle f(x)$ as $\displaystyle x$ approaches $\displaystyle a$: \[ \lim_{x \to a}f(x) = \infty \] means that the values of $\displaystyle f(x)$ can be made arbitrarily large (as large as we please) by taking $\displaystyle x$ sufficiently close to $\displaystyle a$ (but not equal to $\displaystyle a$). Similarly we can define \[ \lim_{x \to a}f(x) = -\infty \] and one-sided limits such as \[ \lim_{x \to a^-}f(x) = \infty {\hspace{1.5in}} \lim_{x \to a^+}f(x) = \infty \]

  

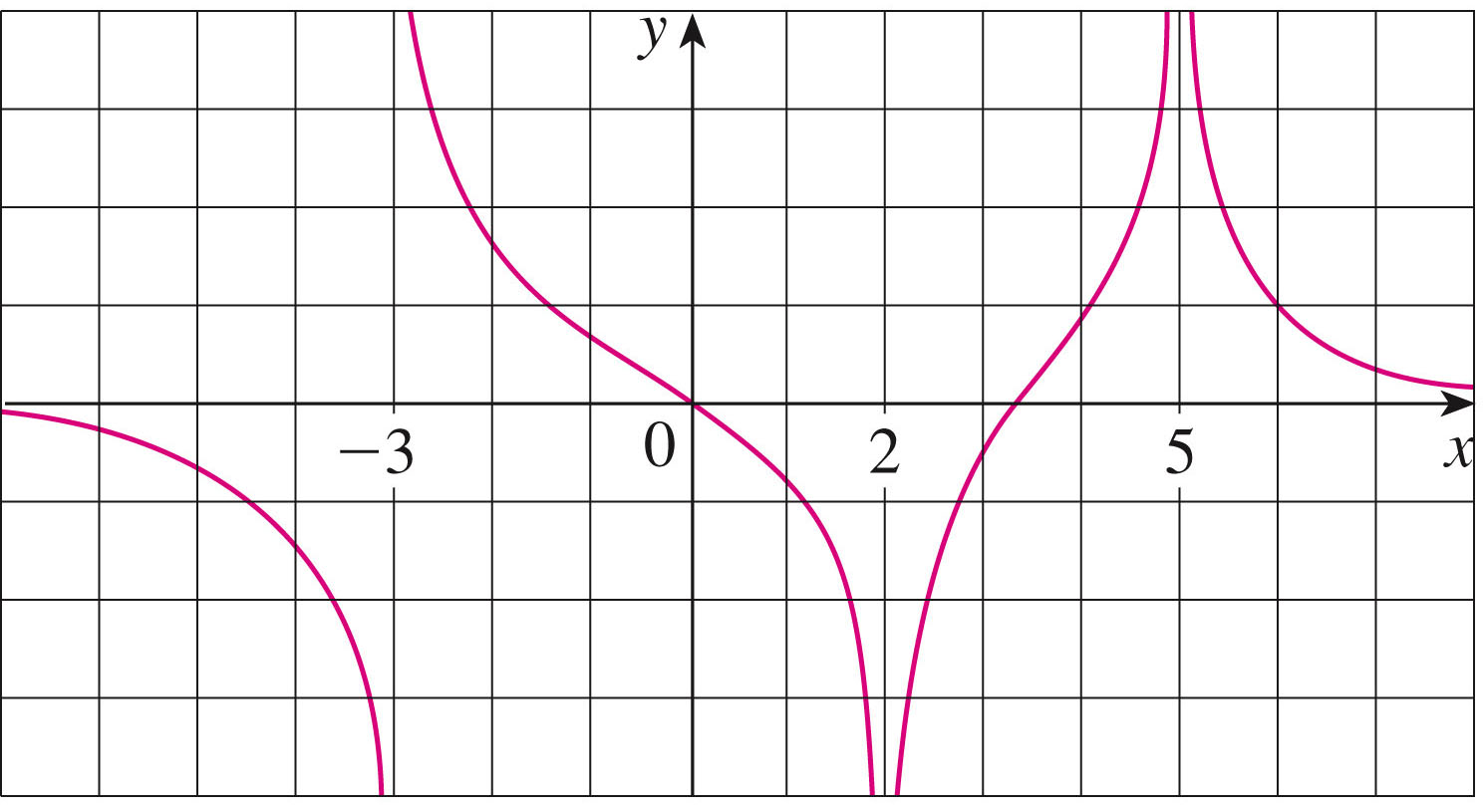
  In any of these cases, we define a vertical asymptote of the curve $\displaystyle y=f(x)$ at $\displaystyle x=a$.