- Reminder that our midterm exam is next Thursday, covering the
first three chapters. We'll review next Tuesday. I'll have some
review material available by our next class.
Remember that you'll be allowed a page of notes; you might want to get that started.
- Quiz next time will be over sections 3.1 and 3.2: recursion and
recurrence relations.
- Quizzes are returned.
- A key
- Theorem: in the domain of the natural numbers, the first
principle of induction can be written this way:
\(P(1) \land (\forall k)(P(k) \rightarrow P(k+1)) \rightarrow (\forall k)P(k)\)
- \((\forall k)(P(k) \rightarrow P(k+1))\) hyp
- \(P(1)\) hyp
- \(P(1) \rightarrow P(1+1)\) 1,ui
- \(P(2)\) 2,3,mp
- \(P(2) \rightarrow P(2+1)\) 1,ui
- \(P(3)\) 4,5,mp
- etc. etc.
- The 1st principle of mathematical induction is like this:
if the kth domino falls, then the (k+1)th domino falls; and since the first domino falls, they must all fall down.The 2nd Principle of mathematical induction is like this:
if every domino up to the kth domino falls, then the (k+1)th domino falls; and since the first domino falls, they must all fall down.Not much difference, is there? They're logically equivalent.
- I chose an induction problem that was featured (and
solved) on p. 114. Perhaps the tricky part was
figuring out how to write the nth odd
number. Like some of the other problems we've looked
at, you look for the pattern:
n nth odd 1 1 2 3 3 5 4 7 5 9 Many of you made use of summation notation to express this, and so the assertion \(P(n)\) would look like this: \[ P(n):\ \ \sum_{i=1}^{n}(2i-1)=n^2 \] Note that the stuff "inside" the summation is a function of \(i\) (not \(n\)), and that \[ \sum_{i=1}^{n}(2i-1)= 1+ 3 + 5 + \ldots + (2n-1) \] and not \[ 1+ 3 + 5 + \ldots + n \] as some mistakenly wrote. The last entry is the \(n^{th}\) odd, not \(n\) itself.
- We wrapped up Section 3.2
(Recurrence Relations), and
- Started on Section 3.3 (Analysis of Algorithms)
- we'll spend a little time with the Euclidean algorithm, which is
described in the text (but may appear somewhat mysterious): The
idea is simple (and recursive): to compute the "gcd(n,m)"
(greatest common divisor) of two positive integers \(m\) and
\(n \gt m\), find the number of times that \(m\) goes into
\(n\) (call the largest such integer \(q\)), and compute the
remainder \(r\):
\[
n=qm+r
\]
Then recurse, based on the fact that
\(gcd(n,m)=gcd(m,r)\).
Notice that both \(r \lt m\) and \(m \lt n\), so the problem is "smaller"; ultimately \(r=0\). At that point, the current value of \(m\) is the gcd.
The Euclidean algorithm is ancient (predating Fibonacci by over a thousand years), and yet it has a fundamental connection to the Fibonacci numbers, which we shall see.
When it comes time, we'll use some graph paper, in order to better understand
- how the algorithm works
- Why \(gcd(n,m)=gcd(m,r)\)
- how to understand the Worst-case scenario: a Fibonacci spiral.
- and how to get the worst-case bound.
- We'll begin with an analysis of binary search, however. In
particular, when is it better to use binary search over a simple
sequential search?
This graph tells the story, and we'll get to it in a bit:
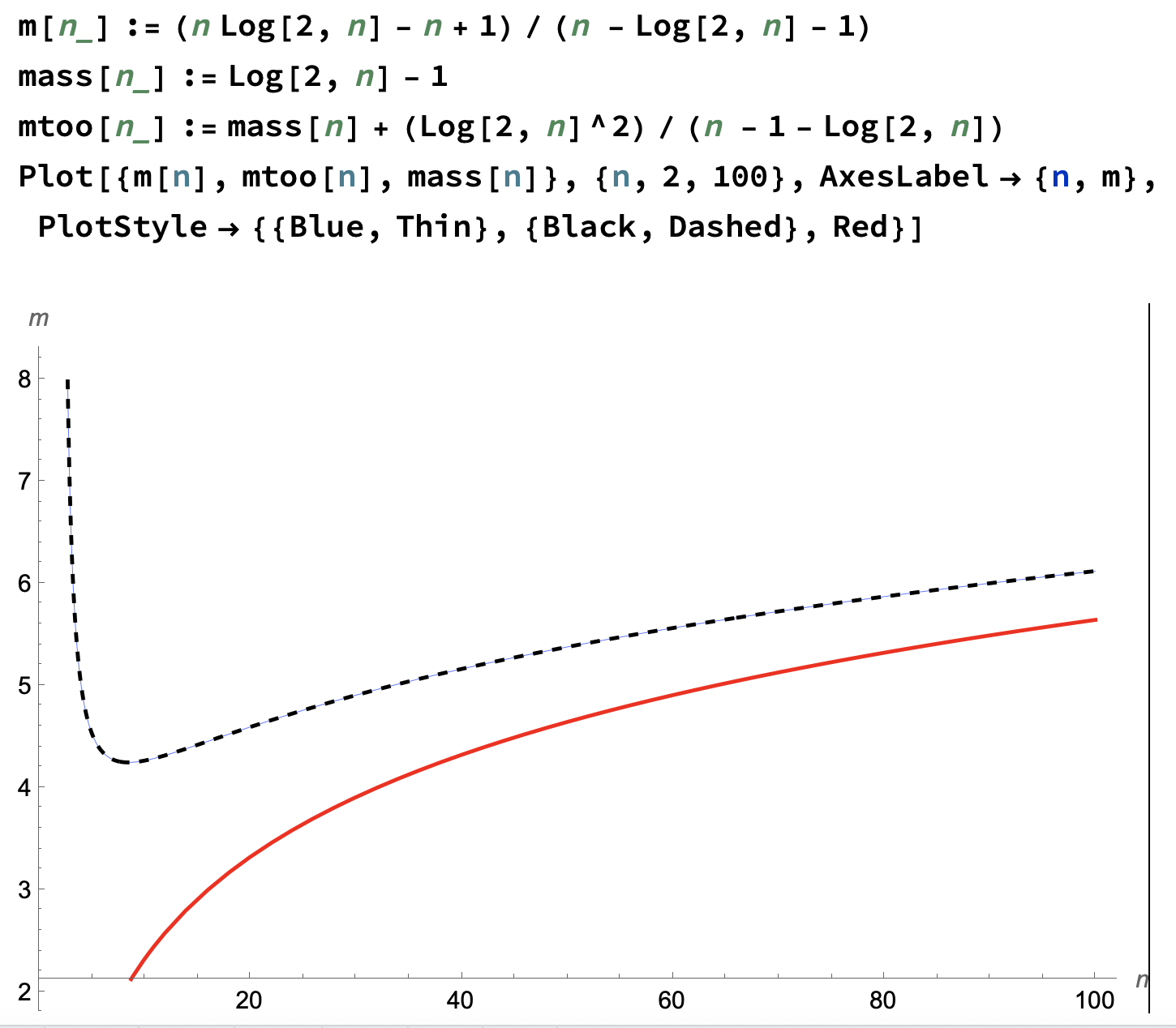
This has to do with how many searches you need to do before it becomes more useful to sort your list with a mergesort and binary search, rather than to simply sequential search.
- If there's much time left, we'll start Section 4.1 (Sets). (Maybe we'll just talk about infinity....)
- Output of my gcd routine
- More on closed-form solutions for Fibonacci numbers (and Catalan numbers, too). Generating functions are an amazing tool.