- Today's quiz will be over symmetry/Platonic Solids. The quiz after
fall break will feature symmetry and wallpaper groups. Our
next topic will be fractals. Still very symmetry-oriented!
- Important: Assignment for your Spring break
You should have some fun, and not think too hard about school! Unless you want to....
When we come back, we'll discuss your projects, and your logos a little more.
- It seems that I can pick up any current issue of Science
and find something to show you relevant to the material in this
class. This week it was Science News;' there are two
things to show you from the current edition:
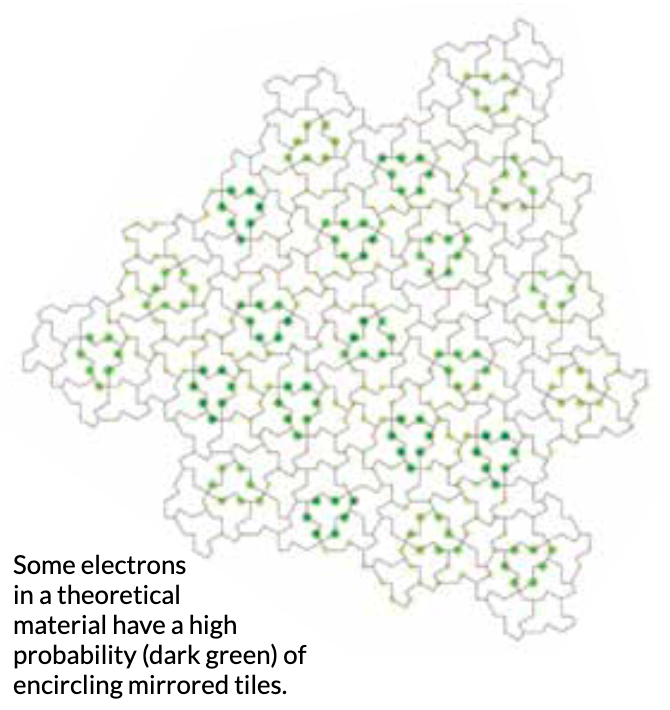
- An
aperiodic tiling using a single "einstein" tile: "That's a
shape that can perfectly cover an infinite plane - no gaps or
overlaps - but only without forming a repeating pattern."
- A molecule
in the shape of a trefoil knot:
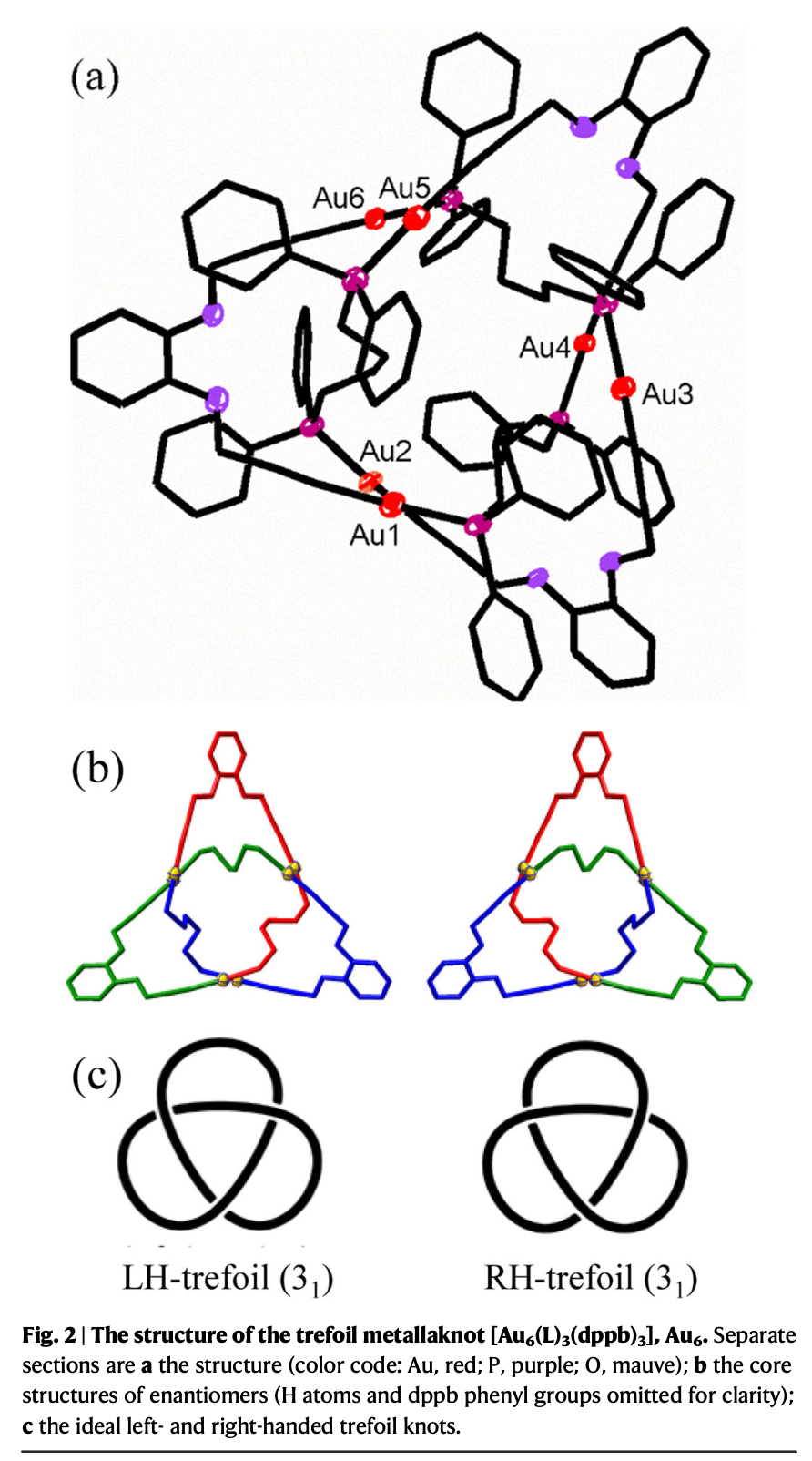
Note, in particular, the "handedness" of the two forms of this molecular knot.
Knots is our next topic after fractals.
That reminded me of a recent article, which described how there are two mirrored types of thalidomide -- "For drug compounds, enantiomers with opposite handedness may have completely opposite effects in the human body. For instance, R-thalidomide is sedative while S-thalidomide is teratogenic..."
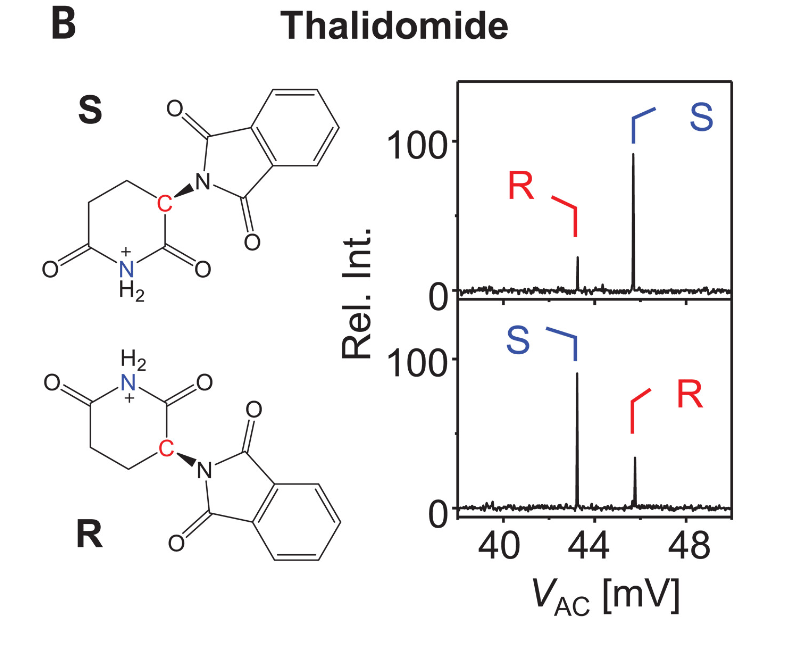
[A few weeks later... Wed May 1 16:00:58 EDT 2024]: There's more to the story: it turns out that the body turns one form into the other randomly, meaning that it's not as though we could manufacture and administer only the "good" variety.....
- An
aperiodic tiling using a single "einstein" tile: "That's a
shape that can perfectly cover an infinite plane - no gaps or
overlaps - but only without forming a repeating pattern."
- Bonus track! Yesterday's Washington Post had an article entitled
How to hang art and photos to please the eye and the brain:
Consider height, symmetry and balance for the most appealing result
They had this to say:
Create balance and symmetry
Research shows that humans prefer symmetry. A 2018 study from the University of Vienna found that both art history and psychology students at the university level prefer symmetrical patterns over asymmetrical ones with art; this may have an evolutionary basis as well as a psychological one, the authors noted. In another series of experiments, researchers in Rome found that visual symmetry even leads to positive mood changes in viewers.
This may be because symmetry creates a sense of order. If a group of paintings "is symmetrical, we perceive it as more thought-through, not random," explains Augustin, whose firm, Design With Science, uses principles from neuroscience to create spaces that foster productivity, well-being and positive mental states. "It creates a certain comfort in us because it's easier to survey and process."
- We undertook three activities:
- Drawing duals of Platonic solids
- Examining the 17 different wallpaper groups
- Thinking about symmetry of scale, via another kind of Fibonacci spiral
We'll quickly revisit two of our activities, and then spend a little more time with wallpapers.
- Just for fun: let's do that last projection, of the dodecahedron in the icosahedral projection
- Finally we'll make the best of a bad situation: when your
checkerboards don't work out (and even when they do....)
This exercise gives us an illustration of symmetry of scale: each "petal" is an exact copy of every other, so we're tiling the floor with a single shape (although it is changing in size).
- Then we'll continue our exploration of the 17 wallpaper groups.
Wallpapers involve translations (e.g. wallpapers), including glide reflections. Here is a nice description of these "Transformations of the plane".
For your homework: explore the 17 patterns, and try to find ways to distinguish them.
This site can help us out a lot! Distinguishing the 17 wallpaper groups. In particular, let's take a look at the glide reflection symmetry.
On the back of Polya's display of the 17 wallpaper patterns you find additional patterns. Can we classify those, according to the choices on the front?
- Some Fibonacci spiralling links:
- Creating The Never-Ending Bloom (the artistry of John Edmark)
- The Art of John Edmark | Talk by Paul Dancstep | Exploratorium: Fibonacci spiral checkerboards (and other symmetries of scale)
- Art-Equals Community (with symmetry):

- A gorgeous video of Prof. Carlo Sequin explaining regular polytopes in all dimensions (of which regular polygons are two-dimensional versions, and Platonic solids are three-dimensional versions -- so there are polytopes in higher dimensions!). Here Vi Hart describes eating four-dimensional polytopes...
- Symmetry, by Hermann Weyl (Princeton University Press, 1952)
- Symmetry of lifeforms on Earth
- A fun reading on symmetry
- All wallpapers
- The best site I've found for distinguishing the 17 wallpaper groups (local copy).
- Wallpapers begin with Transformations of the plane (this from the very informative website Wallpaper Groups (here's a local copy)
- Examples of all 17 wallpapers
- Polya's version of the Wallpapers
- Wallpaper exercises, and a Wallpaper exercise handout.
- Hexagonal Paper