Day 27, MAT115R

• Your quiz on symmetry:
  • Key
  • Median: 6.5

• This week's quiz will cover graphs, platonic, simple, and planar; and Euler formula and Euler paths (plus enemies!).

• We covered some special types of graphs:
  • Simple graphs (which, when connected, may or may not have Euler paths)

    I think of these graphs as Facebooks you can have with a given number of individuals.

    We drew all possible simple graphs (with unlabelled vertices) and with 3 or 4 vertices, discovering that there is a sort of duality in these graphs, too. Here are all the distinctly different simple graphs with four vertices.

  • Planar graphs are graphs that can be drawn such that no two edges intersect.
    • Every Platonic graph can be drawn this way; they are, in fact, simple planar graphs.

    • Planar graphs have Euler's formula attached to them: R-A+N=2.
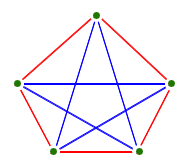
      • the complete graph with five vertices, \(K_5\), is not planar:
        
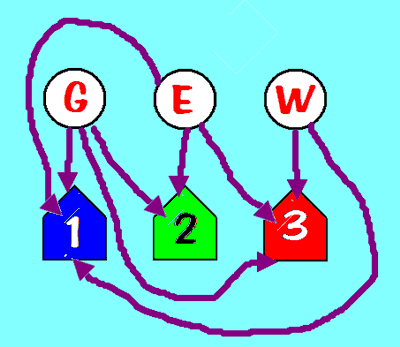
      • The three utilities and three houses graph is not planar:
        

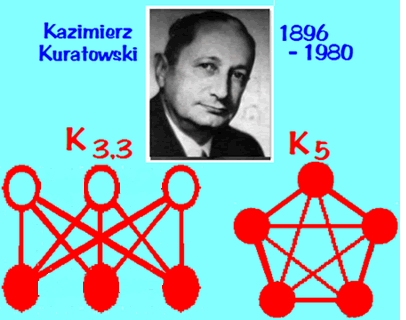
      • Any non-planar graph has a copy of one of these two graphs in it somewhere, as a subgraph:
        

    • Graphs are awfully useful in lots of places in our lives.

      I've assigned you a reading from The Joy of X by Steven Strogatz. Let's talk about is The Enemy of My Enemy (complete graphs, labelled graphs)

      • One focus of this reading is negative numbers. It was the Indians (of Asia) who put negative numbers on a firm foundation (as well as zero), in about the 6th century AD.

        "...you can't see negative 4 cookies and you certainly can't eat them -- but you can think about them...." ("and you have to", says our author).

      • One of the confusing aspects of negative numbers from Strogatz's perspective is that the product of two negative numbers is a positive number.

      • But then Strogatz goes on to use the context of social interactions (negative and positive) to discuss how we maintain stable relationships.

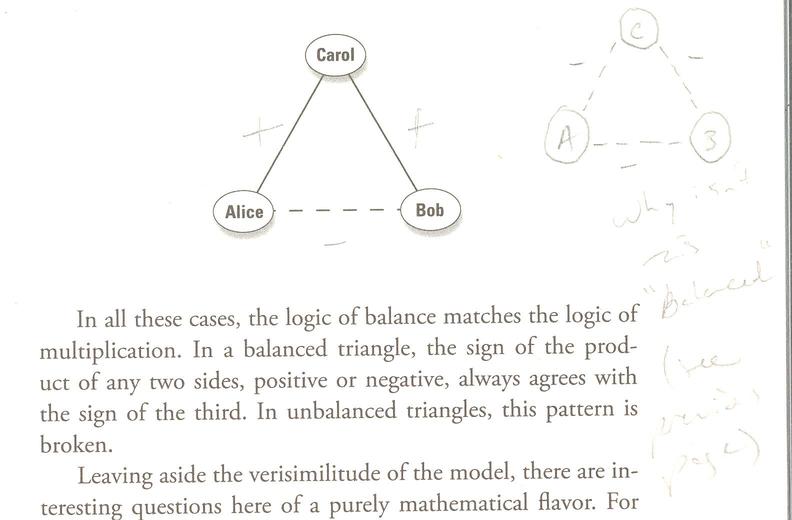
        And the key to understanding stability in three-way social relationships is that the product of two interactions (signified by either +1 or -1) must be equal to the other: so that if two legs are positive, the third in the triangle must be positive; if one leg positive, and the other negative, then the third leg must be negative as well.

        

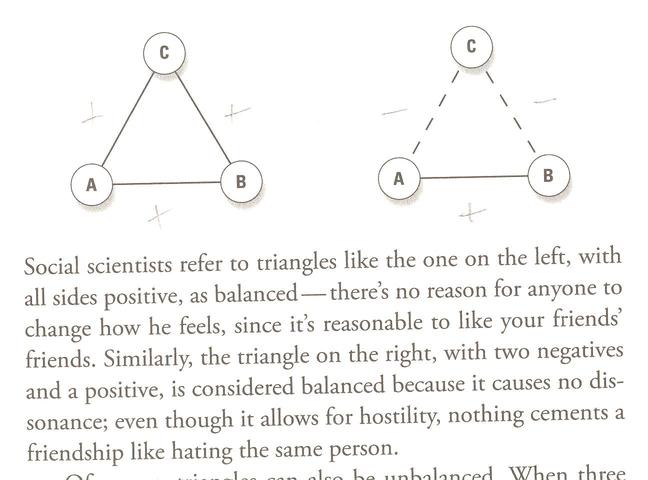
        Strogatz sums up the second case above in the familiar saying that "The enemy of my enemy is my friend".

        The following (two) graphs are unbalanced:

        
        Why is the all negative graph also unbalanced? Because "the enemy of my enemy is my friend!"

        Finally Strogatz shows how historical relationships settled down into this pattern of stability: in "...the run-up to World War I. The diagram that follows shows the shifting alliances among Great Britain, France, Russia, Italy, Germany, and Austria-Hungary between 1872 and 1907."

        

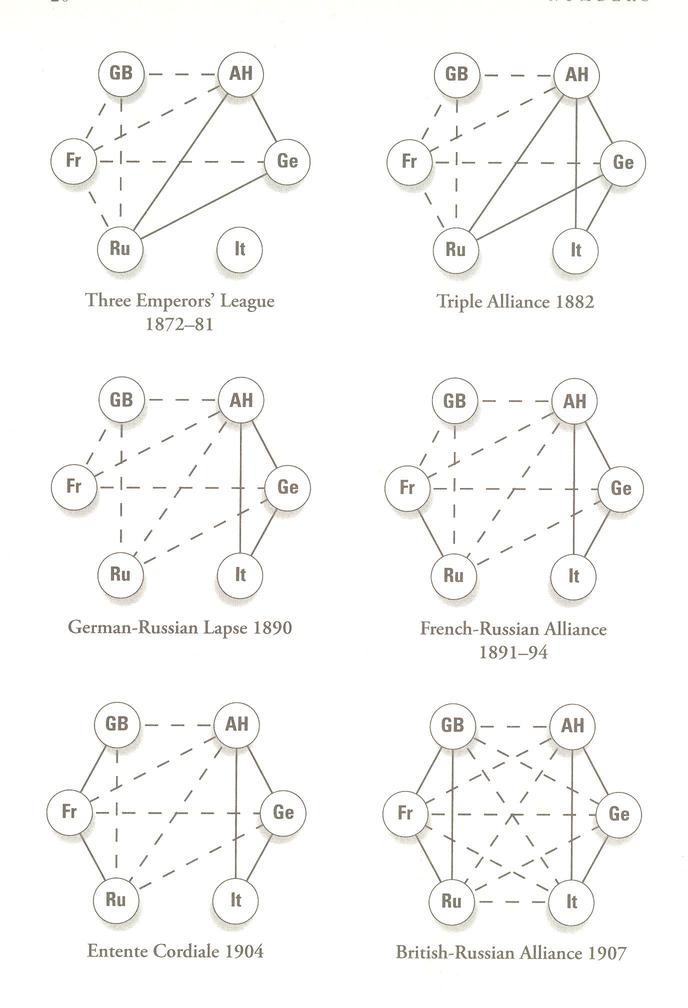
        The bottom right graph (complete!) is the only stable configuration, "...balanced, but on the brink of war."

        Notice that Italy, which was not bothered by any of the powers of GB, F, or Ru, became a target -- because the friend of my enemy is my enemy, too:

        • The enemy of my enemy is my friend: \[ (-1)\cdot(-1)=(+1) \]
        • The enemy of my friend is my enemy: \[ (-1)\cdot(+1)=(-1) \]
        • The friend of my enemy is my enemy: \[ (+1)\cdot(-1)=(-1) \]
        • The friend of my friend is my friend: \[ (+1)\cdot(+1)=(+1) \]

        How do we know that the final graph -- \(K_6\) -- is non-planar? (What does it contain?)

Today we're going to examine fractals in a couple of different contexts, and then talk about how to make a few.

• You've seen fractals in this class already, and hopefully you've heard me mention them. I mentioned them in the context of the Fibonacci numbers, and in the context of the Fibonacci and Golden spirals.

  In the latter two cases, you recall that by constructing spirals with squares in certain ways, we ultimately achieve (or tend to) a golden rectangle, which contains a perfect copy of itself (only smaller): the side lengths are in the ratio $\phi$, where \[ \phi=\frac{1+\sqrt{5}}{2} \approx 1.618 \]

  • Now: what kind of rectangle will you get if you repeat the spiral process with a non-Fibonacci rectangle to start (rather than a 1x1 square)? For example, you might start with a 3x1 rectangle, and then append the biggest square you can each time.

    Turns out, that if you do it over and over and over again, you'll still obtain rectangles that becomes more and more golden!

    But that's because we were adding a square each time. Let's try another process....

  • The A0 Paper Fractal

    "A paper" is something you've no doubt encountered before: it's the long sheets we occasionally use (usually "A4" paper), types of paper far more common in Europe.

    "A paper" is constructed so that, if folded in half (do we say the long way or the short way?), you get a sheet which has exactly the same shape -- that is, the ratio of its side lengths is the same as the original sheet.

    

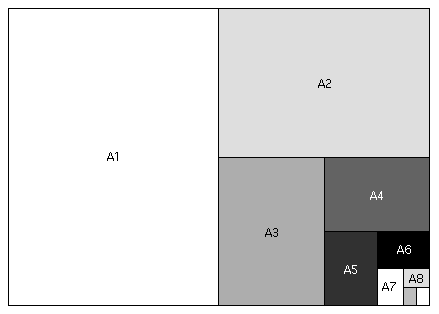
    Let's see what the dimensions of A paper must be so that this requirement is fulfilled....

    Call the long dimension of the A1 paper above $x$, and the short dimension 1.

    • Then the ratio $x:1$ is the same as the ratio $1:\frac{x}{2}$.
    • Solve for $x$: \[ \frac{x}{1}=\frac{1}{\frac{x}{2}} \] and we've got a quadratic equation on our hands! Fortunately this one happens to be particularly easy: \[ x^2=2 \] so $x=\sqrt{2} \approx 1.4142$.

    Let's check: here are the "official" paper sizes (in mm):

    

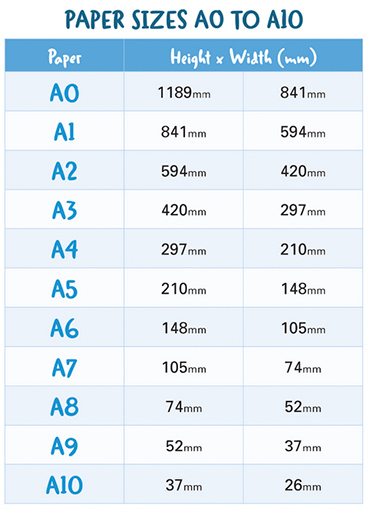
    Pick a height, and divide by the width, and what do you get? Approximately 1.4142.... E.g. A1: $841/594 \approx 1.4158$.

  • Why not an A0 paper spiral? Let's try that.... This is the spiral, created using non-squares ("A-rectangles") each time:
    

    We could go on forever! There's "the world within the world". This is a fractal.

    (By the way, the spiral image above has dimensions 424x300 -- the ratio? 1.4133333333333333....)

  • Fractals
    • The concept of fractals is the most modern mathematics that we study in this course. We've worked our way up from the Babylonians all the way to the 21st century.

      Here is our "intuitive" definition of a Fractal:

      A world within a world!

      By which I mean that there's a perfect copy of the fractal contained, or embedded, within itself -- and perhaps infinitely many!

      In the bulb there is a flower; in the seed, an apple tree; in cocoons, a hidden promise: butterflies will soon be free! In the cold and snow of winter there's a spring that waits to be, unrevealed until its season, something God alone can see. (In the bulb there is a flower)

      For example, in the A0 Fractal, the whole rectangle (A0 paper) contains smaller (but perfect) copies of itself -- A1, A2, A3, .... papers.

      This key notion is more formally called "self-similarity": "a self-similar object is exactly or approximately similar to a part of itself (i.e. the whole has the same shape as one or more of the parts)."

    • Some other examples you have already seen during our course:
      • Dual Platonics: e.g. a tetrahedron within a tetrahedron within a tetrahedron.... Maybe cooler are the other pairs, where we alternate solids (hexa then octa, or icosa then dodeca), then repeat the process:
        

      • This tree diagram of the rabbit problem that gave rise to the Fibonacci numbers is a fractal:
        

      • My "Flirting with Death Spiral" that I created using a little app that I wrote.
        

      • Often these fractals arise out of the idea that we carry out a process, then "do it again, do it again"....

        This goes under the heading of recursion.

    • Here are some examples you might have seen before:
      • Here's a suitable mascot for this unit: Bessie the fractal cow:
        

      • World's Most Famous Fractal discovered/created by the late Benoit Mandelbrot (Novel Mathematician, Dies at 85: 10/14/2010):
        

    • So what is a fractal? A couple of things we'll generally see:
      1. It's a process or graph that possesses "self-similarity".

      2. It often possesses a simple and recursive (or iterative) definition -- that is, we do something, and then we "do it again!"

    • Let's check out a beautiful gallery of natural fractals.

      It turns out that nature loves fractals, just like it loves Fibonacci numbers.

      I found this image in a recent issue of Nature:

      

    • Building deterministic fractals with sticks
      • Consider the famous "Koch" fractal:
        1. Start with a straight stick.
        2. Replace the middle third of the stick with a little "tent" -- two third-length sticks.
        3. Do it again and again!
        4. This triangular paper is good for that. And here's one that's "pre-made" for some triangular fractal creation...
        

        This fractal becomes infinitely long, but in a confined space! Very strange.... but this type of strange behavior is typical of fractals.

        Let's make a variation of that. Use your graph paper, and a stick along the short edge, that's 88 units long. Best to use a pencil with a good eraser! We'll want a stick that's 81 squares long (because we're dividing into thirds).

        Instead of triangular tents, we'll make square tents.

      • Here are some more lovely examples called "L-System Fractals" (including the Koch fractal, but check out the beautiful bushes!).

      • The Sierpinski triangle is an area fractal. We've seen that before, peeking out from within Pascal's triangle!
        • Triangular paper is good for Sierpinski; this triangular paper has more triangles.
        • Let's create one by subtraction.
        • After we're finished removing all that stuff, how much area is left in the triangle?

    • Now let's introduce a little bit of randomness: Sierpinski's triangle again

      The Chaos game - generating fractals using random movement!

      • Once again, simple rules lead to complex objects. This time, however, we don't proceed methodically, but rather haphazardly - and yet we still produce the complex images.

        One of the most interesting fractals arises from what Michael Barnsley has dubbed ``The Chaos Game'' [Barnsley]. The chaos game is played as follows. First pick three points at the vertices of a triangle (any triangle works---right, equilateral, isosceles, whatever). Color one of the vertices red, the second blue, and the third green.

        Next, take a die and color two of the faces red, two blue, and two green. Now start with any point in the triangle. This point is the seed for the game. (Actually, the seed can be anywhere in the plane, even miles away from the triangle.) Then roll the die. Depending on what color comes up, move the seed half the distance to the appropriately colored vertex. That is, if red comes up, move the point half the distance to the red vertex. Now erase the original point and begin again, using the result of the previous roll as the seed for the next. That is, roll the die again and move the new point half the distance to the appropriately colored vertex, and then erase the starting point.

        • with 10 points
        • with 100 points
        • with 500 points
        • with 1000 points
        • with an infinite number of points!
        From randomness comes order; from simple rules comes complicated objects! Then all hell broke loose.

• Triangle and rectangle paper
• Shodor:
  1. Snowflake on-line
  2. Gasket on-line
  3. The Fractal Microscope (click on the image)

• L-Systems in PostScript, from which I generated this image:
  

• Vi Hart
  • Vi Hart draws fractals
• L-System Fractals
• Nice website with examples of Cantor, Koch, and other fractals
• Here are some more lovely examples
• l-system generator: world's simplest math tool
• I first encountered the L-Systems fractals at britton.disted.camosun.bc.ca/fractals_arcytech/lsystems.html, but that's a dead link. However, I copied the files, and have a local copy here. However, web browsers these days don't seem to like the applet tag in javascript, so this doesn't work anymore in a standard web browser...:(