- Thursday's quiz will cover graphs, platonic, simple, and planar; and Euler formula and Euler paths (plus enemies!).
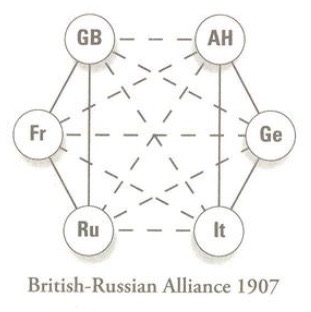
- Last time we talked a lot about an application of graphs featured
in the reading "The enemy of my enemy", in which Strogatz used graphs
-- weighted graphs, with edges that were either "positive" or
"negative" to simultaneously explore the dynamics in the old world
leading up to the first world war,
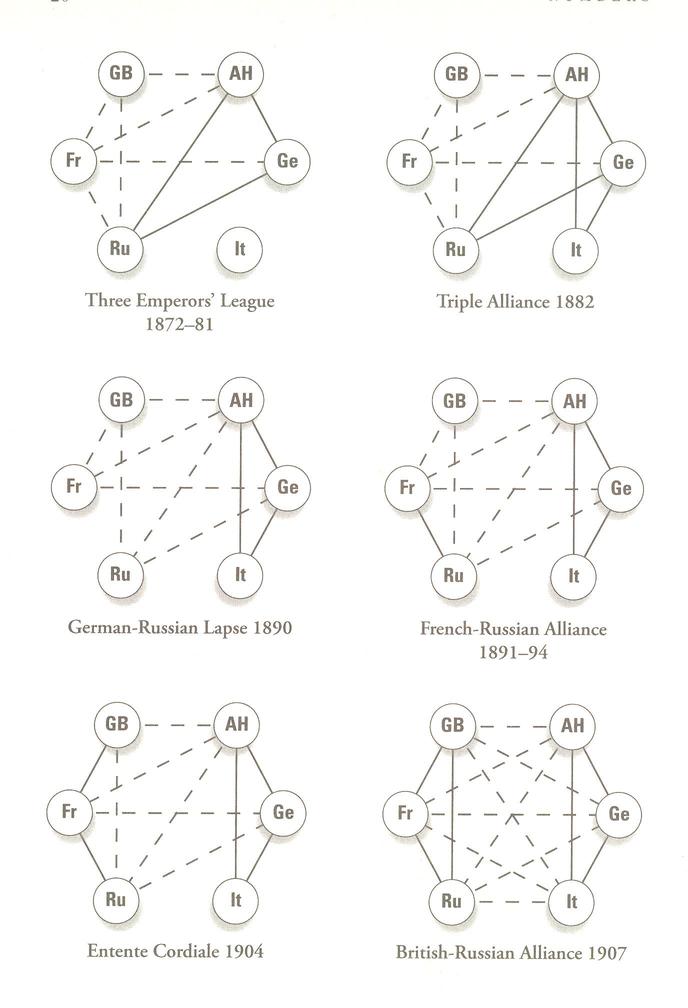
- The enemy of my enemy is my friend: \[ (-1)\cdot(-1)=(+1) \]
- The enemy of my friend is my enemy: \[ (-1)\cdot(+1)=(-1) \]
- The friend of my enemy is my enemy: \[ (+1)\cdot(-1)=(-1) \]
- The friend of my friend is my friend: \[ (+1)\cdot(+1)=(+1) \]
- Planar graphs have Euler's formula attached to them:
R-A+N=2, and we verified it for one of the Platonic
graphs, which are all clearly
planar (since they can be drawn without edge
intersections).
- R: the number of regions, or faces
- A: the number of arcs, or edges
- N: the number of nodes, or vertices
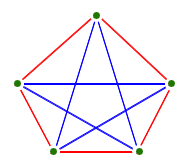
- The simplest non-planar graphs are
- the complete graph with five vertices, \(K_5\), is
not planar:
- The three utilities and three houses graph is not
planar:
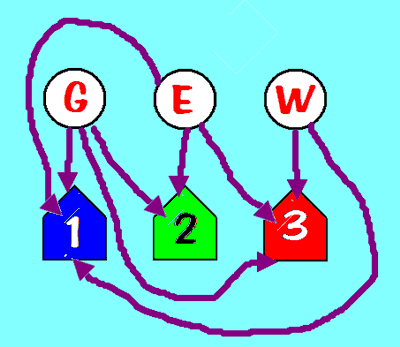
- Any non-planar graph has a copy of one of these two graphs
in it somewhere, as a subgraph:
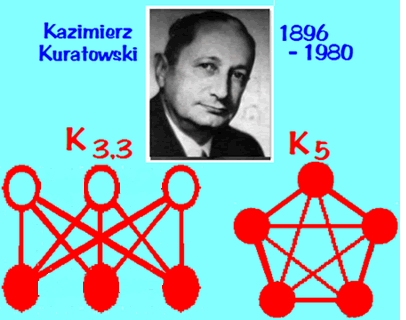
- the complete graph with five vertices, \(K_5\), is
not planar:
- Strogatz's final graph, \(K_6\), has a copy of both \(K_5\) and
\(K_{3,3}\) in it, so it's certainly non-planar:
- We examined fractals in a couple of different
contexts:
- Golden rectangles
- Fibonacci trees
- Dual platonics (e.g. a tetrahedron inside a tetrahedron)
- The A0
Paper Fractal
"A paper" is constructed so that, if folded in half (do we say the long way or the short way?), you get a sheet which has exactly the same shape -- that is, the ratio of its side lengths is the same as the original sheet.
Why not an A0 paper spiral? Let's try that.... This is the spiral, created using non-squares ("A-rectangles") each time:
We could go on forever! There's "a world within a world". This is a fractal.
- Here's a suitable mascot for this unit: Bessie the fractal cow:


- The concept of fractals is the most modern mathematics that we
study in this course. We've worked our way up from the Babylonians all
the way to the 21st century.
- Here is our "intuitive" definition of a Fractal:
-
A world within a world! By which I mean that there's a perfect copy of the fractal contained, or embedded, within itself -- and perhaps infinitely many!
In the bulb there is a flower; in the seed, an apple tree; in cocoons, a hidden promise: butterflies will soon be free! In the cold and snow of winter there's a spring that waits to be, unrevealed until its season, something God alone can see. (In the bulb there is a flower)
For example, in the A0 Fractal, the whole rectangle (A0 paper) contains smaller (but perfect) copies of itself -- A1, A2, A3, .... papers.
This key notion is more formally called "self-similarity": "a self-similar object is exactly or approximately similar to a part of itself (i.e. the whole has the same shape as one or more of the parts)."
- Here are some examples of fractals that you might have never seen before:
- World's
Most Famous Fractal discovered/created by the late Benoit
Mandelbrot (Novel Mathematician, Dies at 85: 10/14/2010):

He transformed the world, by making art this beautiful accessible.
You owe a lot of your fun video games to this guy!
The Fractal Microscope (click on the image) lets you play with his fractals.
- World's
Most Famous Fractal discovered/created by the late Benoit
Mandelbrot (Novel Mathematician, Dies at 85: 10/14/2010):
- So what is a fractal? A
couple of things we'll generally see:
- It's a process or graph that possesses "self-similarity".
- It often possesses a simple and recursive (or iterative)
definition -- that is, we do something, and then we "do
it again!"
- It's a process or graph that possesses "self-similarity".
- Let's check out a beautiful gallery of natural
fractals.
It turns out that nature loves fractals, just like it loves Fibonacci numbers. I found this image in a recent issue of Nature:

Coastlines are fractal in the same way: if you examine them at all scales, they look about the same.
- Building deterministic fractals with sticks
- There are two aspects to creating a fractal:
- Starting with an object (the "initiator"), and then
- Creating a rule that creates new versions of the object inside the object (the "generator").
- An early fractal wasn't really thought of as such:
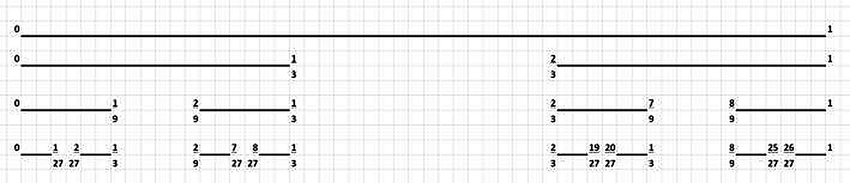
- Start with a straight stick (the initiator).
- Cut out the middle third of the stick.
- Now do it again and again!
- What's happening to the number of sticks?
- What's happening to the total length of all the sticks?
- Consider the famous "Koch" fractal:
- Start with a straight stick (the initiator).
- Replace the middle third of the stick with a little "tent" -- two third-length sticks (the generator).
- Now do it again and again!
- Computer generation of the Koch fractal
- This triangular paper is good for that. And here's one that's "pre-made" for some triangular fractal creation...
This fractal becomes infinitely long, but in a confined space! Very strange.... but this type of strange behavior is typical of fractals.
Let's make a variation of that. Use your graph paper, and a stick along the short edge, that's 88 units long. Best to use a pencil with a good eraser! We'll want a stick that's 81 squares long (because we're dividing into thirds).
Instead of triangular tents, we'll make square tents.
- Here are some more lovely examples called "L-System
Fractals"
(including the Koch
fractal, but check out the beautiful bushes!).
- The Sierpinski triangle is an area fractal. We've
seen that before, peeking out from within Pascal's
triangle! Vi Hart has a nice video about it.

It can also be created from rectangles:

- Triangular paper is good for Sierpinski; this triangular paper has more triangles.
- Let's create one by subtraction.
- After we're finished removing all that stuff, how much area is left in the triangle?
- There are two aspects to creating a fractal:
- Now let's introduce a little bit of randomness: Sierpinski's
triangle again
The Chaos game - generating fractals using random movement!
- Once again, simple rules lead to complex
objects. This time, however, we don't proceed
methodically, but rather haphazardly - and yet we still
produce the complex images.
One of the most interesting fractals arises from what Michael Barnsley has dubbed ``The Chaos Game'' [Barnsley]. The chaos game is played as follows. First pick three points at the vertices of a triangle (any triangle works---right, equilateral, isosceles, whatever). Color one of the vertices red, the second blue, and the third green.
Next, take a die and color two of the faces red, two blue, and two green. Now start with any point in the triangle. This point is the seed for the game. (Actually, the seed can be anywhere in the plane, even miles away from the triangle.) Then roll the die. Depending on what color comes up, move the seed half the distance to the appropriately colored vertex. That is, if red comes up, move the point half the distance to the red vertex. Now erase the original point and begin again, using the result of the previous roll as the seed for the next. That is, roll the die again and move the new point half the distance to the appropriately colored vertex, and then erase the starting point.
From randomness comes order; from simple rules comes complicated objects! Then all hell broke loose.
- Once again, simple rules lead to complex
objects. This time, however, we don't proceed
methodically, but rather haphazardly - and yet we still
produce the complex images.
