- We have an exam next week. It will cover everything since the last
exam, from the Golden rectangle and spiral on.
- Today's quiz will cover graphs, platonic, simple, and planar;
and Euler formula and Euler paths (plus enemies!).
- As I'm getting ready for class, I read this
article about a new agent -- Paenibacillus -- in the fight against
drug-resistant bacteria, and I think to myself -- it looks so fractal!

This bacteria produces a lasso-shaped molecule they named lariocidin.
- Fractals have been around a long time, actually forever (since nature
loves them). But mathematicians have been aware of them since at
least the time of Cantor and Koch (early 1900s):
- But they came into popularity with Benoit Mandlebrot, computer
graphics, and his famous

- We actually created fractals, including the Koch snowflake, the
Sierpinski triangle, and the Danielleski Square (this last one is not
well known).
- We discovered exponential growth and exponential
decay (that is, things grow or decay by a constant factor at each
step).
For example,
- the stick-based Koch fractal grows in number of
sticks by a factor of four at each step (the generator turns a
stick into four sticks). The fractal grows in length at each
step, as well, by a factor of 4/3 (the generator turns three
thirds of a stick into four thirds of a stick).
The stick thus becomes of infinite length as the process continues to infinity, yet the snowflake stays right in front of us. It's infinitely long, but in a finite amount of space. Mind blowing!
- The triangle-based Sierpinski triangle has area removed at each step, and at each step three times as many triangles as in the previous iteration appear. So the number of triangles grows as powers of three, \(3^n\), but the area diminishes by a factor of \(3/4\) each time: \(\left(\frac{3}{4}\right)^n\), and ultimately disappears (leaving the "Sierpinski dust").
- the stick-based Koch fractal grows in number of
sticks by a factor of four at each step (the generator turns a
stick into four sticks). The fractal grows in length at each
step, as well, by a factor of 4/3 (the generator turns three
thirds of a stick into four thirds of a stick).

You're not going to believe this, but Wednesday night I got home to find a set of Santa Dolls on my kitchen table. My aunt recently died, and although someone thought that my wife might like them, I took them instead! To show you.
- A fractal
- It's a process or graph that possesses "self-similarity".
- It often possesses a simple and recursive (or iterative)
definition -- that is, we do something, and then we "do
it again!"
- It's a process or graph that possesses "self-similarity".
- Last time we were building deterministic fractals with sticks, and
triangles, and squares:
- There are two aspects to creating a fractal:
- Starting with an object (the "initiator"), and then
- Creating a rule that creates new versions of the object inside the object (the "generator").
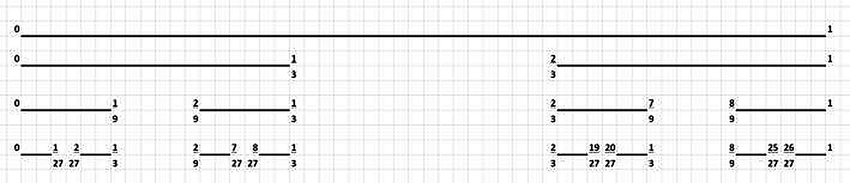
- Start with a straight stick (the initiator).
- Cut out the middle third of the stick.
- Now do it again and again!
- What's happening to the number of sticks?
- What's happening to the total length of all the sticks?
- Consider the famous "Koch" fractal:
- Start with a straight stick (the initiator).
- Replace the middle third of the stick with a little "tent" -- two third-length sticks (the generator).
- Now do it again and again!
- Computer generation of the Koch fractal
- This triangular paper is good for that. And here's one that's "pre-made" for some triangular fractal creation...
This fractal becomes infinitely long, but in a confined space! Very strange.... but this type of strange behavior is typical of fractals.
Let's make a variation of that. Use your graph paper, and a stick along the short edge, that's 88 units long. Best to use a pencil with a good eraser! We'll want a stick that's 81 squares long (because we're dividing into thirds).
Instead of triangular tents, we'll make square tents.
- Here are some more lovely examples called "L-System
Fractals"
(including the Koch
fractal, but check out the beautiful bushes!).
- The Sierpinski triangle is an area fractal. We've
seen that before, peeking out from within Pascal's
triangle! Vi Hart has a nice video about it.

It can also be created from rectangles (much like we did with the Danielleski fractal):

- Triangular paper is good for Sierpinski; this triangular paper has more triangles.
- Let's create one by subtraction.
- After we're finished removing all that stuff, how much area is left in the triangle?
- There are two aspects to creating a fractal:
- It turns out that nature works sort of randomly: it turns out that
Sierpinski's triangle can be generated by randomness!
The Chaos game - generating fractals using random movement.
- Once again, simple rules lead to complex
objects. This time, however, we don't proceed
methodically, but rather haphazardly - and yet
we still produce the complex images.
One of the most interesting fractals arises from what Michael Barnsley has dubbed ``The Chaos Game''. The chaos game is played as follows. First pick three points at the vertices of a triangle (any triangle works---right, equilateral, isosceles, whatever). Color one of the vertices red, the second blue, and the third green.
Next, take a die and color two of the faces red, two blue, and two green. Now start with any point in the triangle. This point is the seed for the game. (Actually, the seed can be anywhere in the plane, even miles away from the triangle.) Then roll the die. Depending on what color comes up, move the seed half the distance to the appropriately colored vertex. That is, if red comes up, move the point half the distance to the red vertex. Now erase the original point and begin again, using the result of the previous roll as the seed for the next. That is, roll the die again and move the new point half the distance to the appropriately colored vertex, and then erase the starting point.
From randomness comes order; from simple rules comes complicated objects.
- Once again, simple rules lead to complex
objects. This time, however, we don't proceed
methodically, but rather haphazardly - and yet
we still produce the complex images.
- Turns out that Pascal's triangle possesses one more secret -- there'a
fractal buried in it!
- We'll use this hexagonal paper,
but instead of actually putting in the values from Pascal's triangle,
we'll put in just zeros and ones: 1 if the number is odd in Pascal's
triangle, we indicated that with a 1; if even, we indicate that with a
0.
But we don't need to calculate the numbers in the triangle to figure out which are 0 and which are 1. The rules are much easier to make Pascal's 1-0 triangle:
- 0+0=0
- 1+0=1
- 0+1=1
- 1+1=0
- Then, when we're done, we'll color in all the zeros with our favorite color -- what do you see appearing?
- We'll use this hexagonal paper,
but instead of actually putting in the values from Pascal's triangle,
we'll put in just zeros and ones: 1 if the number is odd in Pascal's
triangle, we indicated that with a 1; if even, we indicate that with a
0.
