Day 30, MAT115R

Last Time

Next Time

Announcements:
- We have an exam Thursday. It will cover everything since the last exam, from the Golden rectangle and spiral on: symmetry, Platonic solids, graphs, and Fractals will be featured!
- We'll be reviewing tomorrow. Remember to create your Platonic cheat sheets!
  Cut and create Platonic solids out of paper, using this template.
  You will be allowed to use these as a cheat sheet for the next exam. They must be assembled, and you may only use your own.
- Last week's quiz
  - A couple of issues: 11 points, (I thought there were ten), and then a real blunder: I told you to show that K4 is not planar -- but it is! Congrats to Finley, who expressed an appropriate amount of astonishment at having to prove that which is impossible.... :)
    So if I took off any points on your problem 2, I put them back -- for the confusion I'd caused.
  - The Key
  - Problem 1: \(K_5\) and \(K_{3,3}\)
  - Problem 2: \(K_4\) is planar, and the number of regions is 4, arcs is 6, and nodes is 4: \(4-6+4=2\).
  - Problem 3: the key is having either 0 or 2 odd vertices. This graph has four.
  - Problem 4 should have looked familiar. Do you learn from your mistakes? That's what I wanted to discover....
    - Dual: tetrahedron
    - Dual: octahedron
    - Dual: hexahedron (the cube)
    I didn't have you draw the icosahedron or the dodecahedron, because they're a little more trouble. But I did bring some representatives today, including some dodecadolls, and a nice (but very fragile!) dual pair of icosa and dodeca.
- As we move on from Fractals into Knots and Links, I wanted to show a couple of fascinating fractal images:
  
  These are an example of Romanesco broccoli -- a fractal in nature! I have tried to grow this, but have not succeeded. I have, however, eaten it! And it's yummy, but really too pretty to eat....:)
Last time:
- We had a review of stick and triangle fractals, that work with
  - an initiator -- the base object, and
  - a generator -- a process from turning initiators into more initiators
  Then you "do it again", of course.
- We discussed "Exponential growth" and "Exponential decay" -- the number of objects often increasing quickly to a huge number, and sometimes the length or area increasing or decreasing exponentially as well.
  The Koch snowflake length increases to infinity, by a factor of 4/3 each time; the Cantor middle third fractal decreases in length each time by a factor of 2/3.
- Then we created a familiar fractal (Sierpinski's triangle) in two new and curious ways:
  - Using a simplified version of Pascal's triangle, we colored the even numbers in the triangle one color, and the odds another.
  - Then we created it randomly, using "the Chaos game": Gasket on-line
  - Both of these methods contrast with doing it by subtraction of areas from an equilateral triangle.
Today's Question of the Day:

What's "the band that never ends"?
Today's new topic is Mobius (and other twisted) bands, which will be followed next time with more general links and knots.
- Mobius bands are a part of geometry, but relate to a special area called "topology" -- the study of form and shape.
  The Topologist's favorite riddle is this: What's the difference between a donut and a coffee cup?
  Answer: There isn't any! (to a topologist....)
- What is a Mobius band?
  - Let's make some!
  - A mobius band is made from a regular band using only a single twist.
  - By the way, did you know that there are two different Mobius bands? They're mirror images of each other! (Symmetry, again....)
    Make one of each! When you connect it, think of screwdrivers: righty tighty and lefty loosy:
- Drawing on a band: draw a "center line" down the middle of your band. What happens? Remember to just stay on one side!
- Properties of a mobius band:
  - A mobius band has only one side.
  - A mobius band has only one edge.
- Cutting a band:
  - What happens when you cut a mobius band "in half"? Check out a bug on a band....
  - Cut that "half" in half again: what happens?
  - What if you cut a mobuis into "thirds"?
  - Other bands:
    - What if you cut a twice-twisted band?
      You get a link!
    - What if you cut a thrice-twisted band?
      You get a knot!
    - If you keep twisting (four times), you'll create something that the ancient Romans certainly knew about, and found lovely:
      
      Solomon's "knot" (we'll see why this is poorly named, and why I use quotes!). Here it is, in context.
    - And the most we'll ever twist together is five times, resulting in the third of the five (simplest) knots we study.
- Applications of Mobius bands:
  - Conveyor belts
  - Kazakhstan's National Library in Astana (still on the drawing board, since 2009! :( )
  - Recycling Topology:
    - The official recycling symbol is mobius, but over time an alternative has crept in:
      
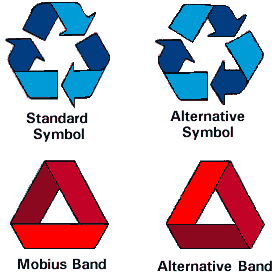
      One of these has rotational symmetry: which one?
    - Mobius, or only Seemingly Mobius?
    - My dad loved mobius bands so much....
    - a history of the recycling symbol (and an AARP article on the history of the creation of the recycling symbol).
  - A joke: "Why did the chicken cross the Mobius band?"
  - Vi Hart's Mobius Music Box: for playing Mobius music.
- Our next topic is links and knots. How does the Mobius band relate to these?
  - Draw the edge of a Mobius band. (Maybe we can get a good artist to do it!)
  - Draw the edge of a twice-twisted Mobius band.
  - Draw the edge of a thrice-twisted Mobius band.
  This class of objects will lead us to the notions of links and knots....
Links
- Triangle and rectangle paper
- Shodor:
  1. Snowflake on-line
  2. Gasket on-line
  3. The Fractal Microscope (click on the image)
- L-Systems in PostScript, from which I generated this image:
- Vi Hart
  - Vi Hart draws fractals
- L-System Fractals
- Nice website with examples of Cantor, Koch, and other fractals
- Here are some more lovely examples
- l-system generator: world's simplest math tool
- I first encountered the L-Systems fractals at britton.disted.camosun.bc.ca/fractals_arcytech/lsystems.html, but that's a dead link. However, I copied the files, and have a local copy here. However, web browsers these days don't seem to like the applet tag in javascript, so this doesn't work anymore in a standard web browser...:(

Website maintained by Andy Long . Comments appreciated.

Fibonacci's solution in Liber Abaci,, chapter 12:
Because the above written pair in the first month bore, you will double it; there will be two pairs in one month. One of these, namely the first, bears in the second montth, and thus there are in the second month 3 pairs; of these in one month two are pregnant and in the third month 2 pairs of rabbits are born, and thus there are 5 pairs in the month; ...
there will be 144 pairs in this [the tenth] month; to these are added again the 89 pairs that are born in the eleventh month; there will be 233 pairs in this month.
To these are still added the 144 pairs that are born in the last month; there will be 377 pairs, and this many pairs are produced from the abovewritten pair in the mentioned place at the end of the one year.
You can indeed see in the margin how we operated, namely that we added the first number to the second, namely the 1 to the 2, and the second to the third, and the third to the fourth and the fourth to the fifth, and thus one after another until we added the tenth to the eleventh, namely the 144 to the 233, and we had the abovewritten sum of rabbits, namely 377, and thus you can in order find it for an unending number of months.