Day 40, MAT115R

• Infinity is NaN: Not a Number

  Natural numbers are things which have a size, and if you add one to a natural number, you get a bigger number.

  You don't get "a bigger number" -- more hate -- when you hate someone "infinity plus one".

  In part because you don't have a number to begin with; but trying to add a number (1) to NaN doesn't work to give you a bigger number.

• Infinity is NaS: Not a Size, either! The reason is that there is more than one size of infinity! This is the most important thing I want you to remember. (This fact will allow you to win on the playground!;)

• The natural numbers are infinite in number (the size of the set is larger than any natural number). It is called a countable infinity, because, well, we can start counting it! (We just never get to the end).

• What is Cardinality? It is the way that we measure infinite sets:

  Two sets have the same cardinality if there is a one-to-one correspondence between them.

  Intuitively: We will say that two sets have the same size if they have the same cardinality.

1. The place is packed, and one person shows up;

   One-to-one correspondence: \(\mathbb{N} \to \{2,3,4,\ldots,n,\ldots\}\), by \[ n \to n+1 \]

   This result informs us that when someone on the playground hollers "I hate you infinity plus 1!", they really haven't hated any more than a simple infinity.

   Alternatively, if your lover says they love you infinitely much, you can't impress them by saying that you love them infinitely plus one. They will scoff, and perhaps leave you for a better mathematician! So take note....

2. The place is packed, and an infinite school bus shows up.

   One-to-one correspondence: \(\mathbb{N} \to \{2,4,6,\ldots,2n,\ldots\}\), by \[ n \to 2n \] We send the people in their rooms to twice their room number.

   Then we slide the students on the bus into rooms \[ n \to 2n-1 \]

   One-to-one correspondence: \(\mathbb{N} \to \{1,3,5,\ldots,2n-1,\ldots\}\).

   This result informs us that when someone on the playground hollers "I hate you 2*infinity!", they really haven't hated any more than a simple infinity.

   The natural numbers have the same cardinality as the set of even natural numbers, and the same cardinality as the set of odd natural numbers.

3. The place is packed, and an infinite number of infinite school buses show up! (Buses numbered 1, 2, .... with seats labelled 1, 2, ....)

   One-to-one correspondence: Each bus gets mapped to a prime number \(\mathbb{N} \to \{2,3,5,\ldots,p_n,\ldots\}\), so that the bus \(m\), \(B_m\), gets mapped to the \(m^{th}\) prime number: \[ B_m \to p_m \] Then the kids on bus \(B_m\) get mapped to powers of that prime: \[ n \to p_m^n \]

   Because of the prime factorization theorem, which says that every natural number (other than 1) is either prime, or can be written as a product of primes in a unique way, we know that two students cannot be assigned to the same room number. If so, we would have two different prime factorizations of the same number, i.e.

   \[ p_r^s=p_m^n \]

   But since prime factorizations are unique, and so that can't happen, every student has their own private room. I hope that the chaperones are ready for this! :)

   This result proves that there are just as many rational numbers (ratios of integers, of the form \(\frac{m}{n}\)) as there are natural numbers.

The real numbers (containing both the rational and irrational numbers) is just too big for Hilbert's Hotel. Mathematicians' guts lead them to believe (generally) that the real numbers are the next largest infinity (the first "uncountable" one).

Let me try to convince you of that, in the following way (called "Cantor's diagonalization argument"):

• Assume that all of the real numbers have found a room at Hilbert's Hotel -- i.e. that there exists a one-to-one correspondence between the natural numbers and the real numbers.
• We'll produce a real number that doesn't have a room. I.e., we'll contradict the assumption, and show that there isn't a one-to-one correspondence.
• We'll do that by constructing a real number that is clearly different from every number on the list of occupants at the hotel.
• The upshot: this means that the natural numbers and the real numbers are not the same size, and that the real numbers are simply too numerous for Hilbert's Hotel.
• The natural numbers have cardinality \(\aleph_0\), and the real numbers have cardinality \(\aleph_1\) -- the next bigger infinity.

Let me show you how.....

1. Some mathematical facts:

   Mathematical facts zero:

   A set \(S\) is just a collection of objects; and a subset of \(S\) is just what you'd expect: some members of \(S\).

   1. It may be all the members, in which we call it an "improper" subset (that is \(S\) is a subset of itself); or
   2. it may be none of them (in which case we call it the empty set, denoted \(\{\}\) or \(\emptyset\)).

   We often denote a set by using braces, e.g. \(S=\{1,2,3\}\) is the set of the first three natural numbers. Thus we would say that \(S\) is a subset of the natural numbers \(\mathbb{N}\), and we denote it \(S \subseteq \mathbb{N}\).

   We say that \(a\) is an element of \(S\) if \(a\) is contained in \(S\), and we write \(a \in S\). So \(1 \in S\), \(2 \in S\), and \(3 \in S\). We deny that an object is in \(S\) this way: \(4 \notin S\).

   Thus for every set, \(S \subseteq S\) and \(\{\} \subseteq S\).

   Mathematical fact one:

   A subset is never bigger in size than the set itself.

   And if the sets are finite, the proper subset is always smaller, but if the set is infinite, we may actually be able to throw away elements of a set and not change the size of the set!

   Mathematical fact two:

   Let's call the set of all of a set S's subsets its power set, \(P(S)\). Pascal's triangle (that rascal!) shows you how many of each type of subset you have (for finite sets). Let's look at "line 3" (that is, 1 3 3 1):

   

   It's about how many ways we have of choosing \(r\) things from \(n\), right? That's exactly what a subset of \(r\) elements is: a choice of \(r\) things from \(n\). Here are the four different groups of subsets represented by that line:

   

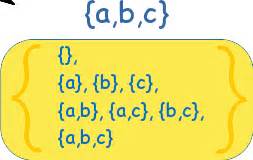
   Mathematical fact three:

   The power set of a set of $n$ elements contains $2^n$ elements.

   Imagine that each of the \(n\) elements is a person, who decides if they're going to stand up and join a subset, or not. Each person has two choices, and they make them independently. Thus we have \(2 \cdot 2 \cdot \ldots 2\) -- \(n\) times -- ways of making a choice of a subset, of choosing.

   (We know that since each row of Pascal's triangle adds to a power of 2, and the elements in each row represent all the different subsets of each size possible, from 0 up to \(n\).)

2. Even the set containing no elements has one subset -- the set itself. So the power set has one element -- has size bigger than the set itself.

   This property holds true for all finite sets -- and it turns out to be true for infinite sets, too!

   Here's a silly video to illustrate how the power set grows with sets of increasing size. (Thanks to Dr. Towanna Roller (Asbury University) and her daughter Kristyn Roller (UK) for this one!)

3. This means that, although the natural numbers $1,2,3,\ldots$ is infinite as a set, there's a bigger set (the power set of the natural numbers).

   And the power set of that set is bigger yet, and so on forever, forever, Hallelujah, Hallelujah!

4. Upshot: infinity comes in various sizes! Infinitely many, in fact. Crazy sounding, I know -- but it's true.

   That symbol that you've been familiar with for all your lives, $\infty$: you thought it stood for a single thing; but it stands for a whole collection of monstrously big things, all too big to really think about properly. (Well, Cantor did!:)

5. That's too crazy, it seems; but, nonetheless, mathematicians know that it's true, because we can prove it! The key to determining if two sets have the same size is the one-to-one correspondence -- and that is key for infinite sets, as well.

6. So, in the end, here's what you say on the playground, when you want to love your friend more:

   "I love you more than the power set of your set of infinite love."

   

   Amen!