- Your test revisions are due today.
- Your quiz today will cover section 2.2.
- Here is the 2.2 worksheet key, and the 2.2 homework key.
- I'll be zooming this meeting, and recording it, for a student who
has a legitimate issue requiring it.
- We obtained the derivative of tangent easily as the derivative of
a quotient:
\[
\tan'(x) = \left(\frac{\sin(x)}{\cos(x)}\right)' = \frac{1}{\cos(x)^2} = \left(\frac{1}{\cos(x)}\right)^2 = \sec(x)^2
\]
and we verified that it made sense, in terms of its graph.
- We observed that we could get the derivative of cotangent "for
free", by symmetry: contangent is just tangent reflected over the
x-axis, followed by a translation:
\[
\cot(x) = -\tan\left(x+\frac{\pi}{2}\right)
\]
So its derivative will just be a reflected and shifted version of
tangents derivative:
\[
\cot'(x) = -\sec\left(x+\frac{\pi}{2}\right)^2 = -\csc(x)^2
\]
Periodicity and symmetry are useful, yes?
Here's is a key for the 2.4 worksheet. Do you see the shifts, and reflections?
We discover how to compute derivatives of compositions of functions, using The Chain Rule (section 2.5).
The chain rule is so critically important because of the importance of compositions of functions.
- The example we just looked at is an example of a composition of functions:
\[
\cot(x) = -\tan\left(x+\frac{\pi}{2}\right)
\]
The computation of cotangent can be accomplished by first an affine
transformation -- \(x+\frac{\pi}{2}\) -- followed by an application of
tangent, and finally a multiplication by -1. If we define
\[
g(x)=x+\frac{\pi}{2}
\]
and
\[
f(x)=-\tan(x)
\]
then we can define cotangent as
\[
\cot(x)=f(g(x))
\]
I like to talk about "x going on a voyage", passing first by \(g\) and
then, transformed by the experience, undergoing transformation by \(f\)
-- finally becoming \(\cot(x)\). A metamorphosis!
- So now, the question becomes: can we figure out the derivative of
a composition, like \(f(g(x))\), if we know the derivatives of \(f\)
and \(g\)? (Yes! -- via the chain rule....)
We will first derive the chain rule, then see how to make use of it.
I'd like to motivate (rather than prove) the chain rule, using the limit definition of the derivative. Everything comes from that!
Our motivation relies on the discrete approximation to the limit definition: \[ g'(x) = \lim_{h \to 0} \frac{g(x+h) - g(x)}{h} \approx \frac{g(x+h) - g(x)}{h} \] and so we can solve (approximately) for \[ g(x+h) \approx g(x) + hg'(x) \] (think of this as the local linearization at every point where \(g\) is differentiable).
Let's now use the limit definition in the case that \(F(x)=f(g(x))\) to derive the chain rule....
- Sometimes there is more than one way to look at a function, and it
pays to look for the simplest form for the stated task: for example, in
the chain
rule preview, we find the function
\[
r(x)=\left(\tan(x)\right)^2
\]
Looks like a composition is most appropriate, but we can also think of
$r(x)$ as
\[
r(x)=\tan(x)*\tan(x)
\]
The product rule works!
Let's take a look at a few more of the compositions in the preview: the chain rule is about differentiating function compositions, and the steps involve
- identification (of the functions making up the composition)
- knowing the derivatives of the component functions
- $h(x) = \tan(2^x)$
- $m(x) = e^{\tan(x)}$
- $z(x) = \sqrt{\tan(x)}$
- Theorem (the chain rule): If $F(x) = f(g(x))$, and both $f$ and $g$ are
differentiable at $x$, then
\[
F^\prime(x) = f^\prime(g(x))g^\prime(x)
\]
I personally think about the chain rule this way:
"f prime of stuff times the derivative of the stuff"; or where $f$ is the "outside" function (so $g$ is the "stuff"):"f prime of stuff times stuff prime.",
\[ F^\prime(x) = f^\prime(stuff)stuff^\prime \]
You can see that the rule is fairly simple, once you've identified the composition -- that is, once you've torn apart $F$ to find $f$ and $g$.
You might want to take a look at this summary from my pre-calc class to review compositions.
- The chain rule looks a little different in Leibniz notation, but
you may see it written this way, too: if we let $y=F(x)=f(u)$, where
$u=g(x)$, then
\[
F'(x)=\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}
\]
This alternative version of the formula helps us to remember that $x$
is going on a journey, passing first through $g$ to become something
new $(u=g(x))$, and then continues on as $u$ through the function $f$
to become $y=f(u)$. It's a metamorphosis. It should be called
the "metamorphosis rule", if there were any justice in the world....
- So let's look at the example above:
\[
\cot(x)=f(g(x))
\]
where \(g(x)=x+\frac{\pi}{2}\) and \(f(x)=-\tan(x)\).
The chain rule says that \[ \cot'(x)=f'(g(x))g'(x) = -\sec\left(x+\frac{\pi}{2}\right)^2\left(x+\frac{\pi}{2}\right)' \] Simplifying, we obtain \[ \cot'(x)= -\sec\left(x+\frac{\pi}{2}\right)^2=-\csc(x)^2 \] as expected.
- The difficulty is often identifying the composition. We'll try
some easy ones first, then get to some ugly ones.
- Examples (from Stewart's
Calculus): tearing apart functions:
- $F(x)=\sqrt{1-2x}$
- $F(x)=6\cot(nx)$
- $F(x)=4 + 0.35 \sin(2 \pi t / 5.4)$
- Trickier: $F(x)=\sin(\sqrt{1 + x^2})$
- A sample problem involving compositions: model the seasonal variation in Keeling's CO2 data:
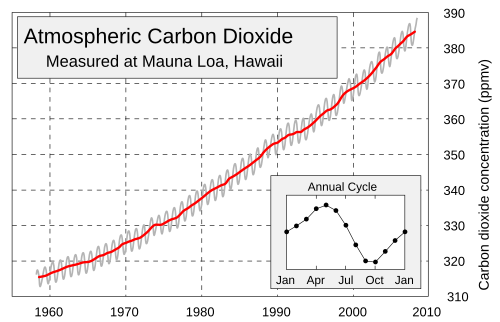
- Keeling data with models: