- Your test revisions are not reviewed yet -- hopefully by Wednesday.
- Your quiz this week will cover the chain rule, section 2.5.
- I've got copies of chain rule notes (and some of the previous notes) scanned here.
- I'll be zooming this meeting, and recording it, for a student who
has a legitimate issue requiring it.
- Out of curiousity (and encouragement), is anyone making use of The Math & Stat Lab? It's free, you know, and there are some really good students working in there... and it's near my office, if you want to stop by!
- We reviewed derivatives of the other trig functions, and noted
that we could express some as translates and reflections of
others. That is, we expressed them as compositions.
- The Chain Rule is all about computing derivatives of
compositions of functions, and is so critically
important because of the importance of
compositions of functions. We'll see an important
example today.
- Compositions such as \(f(g(x))\) are like "x going on a voyage",
passing first by \(g\) and then, transformed by the experience,
undergoing transformation by \(f\) -- finally becoming
\(f(g(x))\). A metamorphosis!
You might want to take a look at this summary from my pre-calc class to review compositions. Generally the hardest thing is identifying the functions making up the composition.
- We derived the chain rule using the limit definition of the
derivative, from a discrete approximation to the limit definition,
\[
g(x+h) \approx g(x) + hg'(x)
\]
(think of this as the local linearization at every point where
\(g\) is differentiable). Here's a little snippet of
Mathematica to illustrate.
- We observed that we can differentiate
\[
r(x)=\left(\tan(x)\right)^2
\]
as a composition, or using the product rule. It's nice to have
options! Choose the easier one...:)
- Then we had a quiz.
- The Quiz:
- Key (here's mine)
- Median: 5.5
- Observations:
- Remember that I told you that there are just three trig identities you should know? I was checking to see who knew the third, and the answer was not many. Two of you did, however: \[ \cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b) \] I hope that you'll remember it now, as well as its partner \[ \sin(a+b)=\sin(a)\cos(b)+\sin(b)\cos(a) \] and the Pythagorean identity, \[ \sin(x)^2+\cos(x)^2=1 \]
- The derivative was straightforward, if you remembered your rules for sine and cosine, and the constant multiple, and the difference rule.
- The derivative rule
\[
\sin'(x)=\cos(x)
\]
only works if \(x\) is expressed in radians. If
you have your calculator available, change from degree
mode to radian mode.
The reason that I chose the value of \(\frac{\pi}{2}\) as the point about which to do the local linearization is because sine and cosine values are "obvious" there:
- Theorem (the chain rule): If $F(x) = f(g(x))$, and both $f$ and $g$ are
differentiable at $x$, then
\[
F^\prime(x) = f^\prime(g(x))g^\prime(x)
\]
I personally think about the chain rule this way:
"f prime of stuff times the derivative of the stuff"; or where $f$ is the "outside" function (so $g$ is the "stuff"):"f prime of stuff times stuff prime.",
\[ F^\prime(x) = f^\prime(stuff)stuff^\prime \]
You can see that the rule is fairly simple, once you've identified the composition -- that is, once you've torn apart $F$ to find $f$ and $g$.
- Examples (from the chain
rule preview): let's compute some derivatives. There are basically
two things to do:
- identify the functions making up the composition; and
- know/discover the derivatives of the component functions.
- $h(x) = \tan(2^x)$
- $m(x) = e^{\tan(x)}$
- $z(x) = \sqrt{\tan(x)}$
- The chain rule looks a little different in Leibniz notation, but
you may see it written this way, too: if we let $y=F(x)=f(u)$, where
$u=g(x)$, then
\[
F'(x)=\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}
\]
This alternative version of the formula helps us to remember that $x$
is going on a journey, passing first through $g$ to become something
new $(u=g(x))$, and then continues on as $u$ through the function $f$
to become $y=f(u)$. It's a metamorphosis. It should be called
the "metamorphosis rule", if there were any justice in the world....
- Further examples:
- $F(x)=\sqrt{1-2x}$
- $F(x)=6\cot(nx)$
- $F(x)=4 + 0.35 \sin(2 \pi t / 5.4)$
- Trickier: $F(x)=\sin(\sqrt{1 + x^2})$
- A sample problem involving compositions: model the seasonal variation in Keeling's CO2 data:
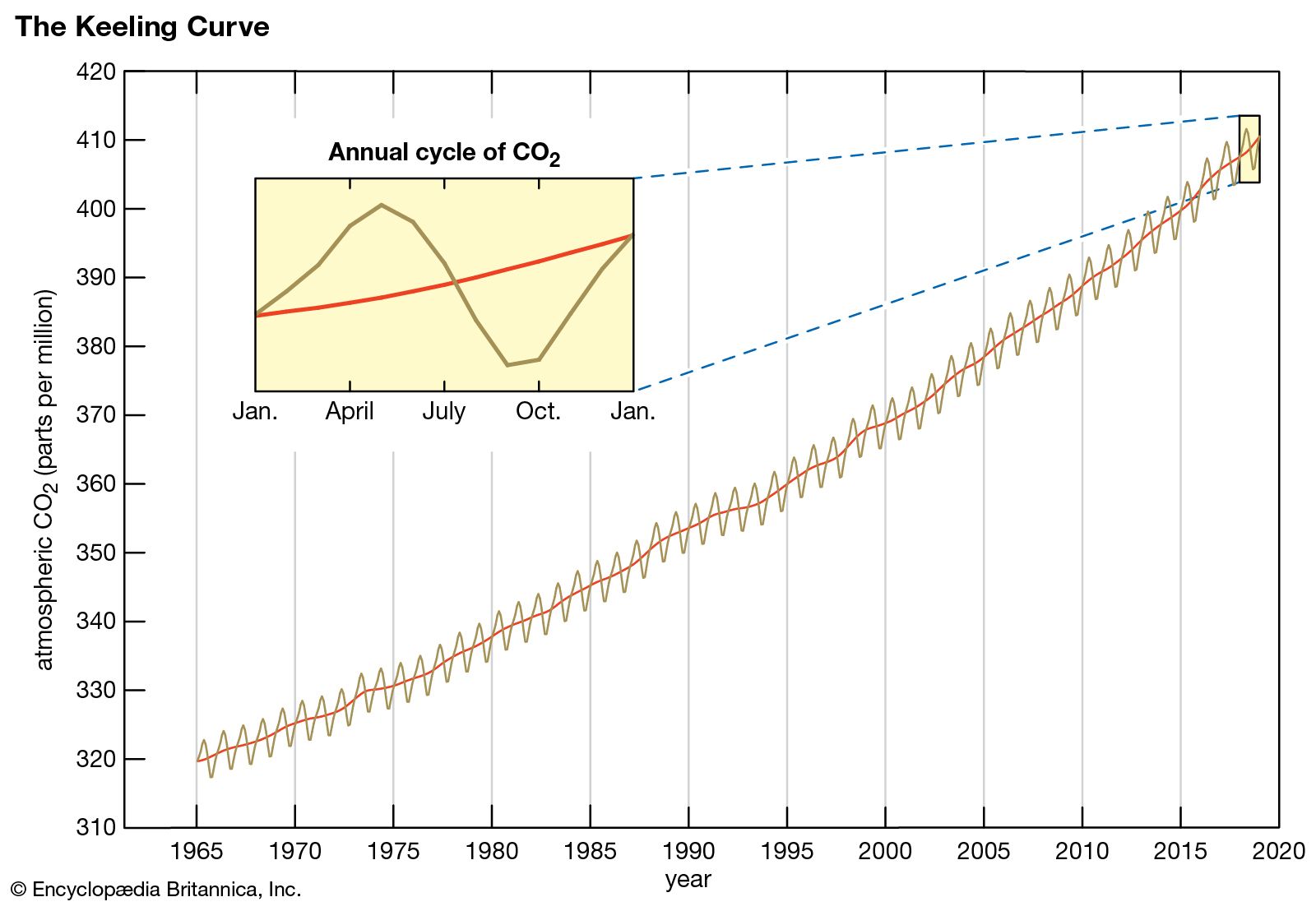
- Keeling data with models:
- A summary from another class: The Chain Rule
- A Keeling Analysis in Mathematica
- The latest Keeling data