- The quiz this week will be over the derivatives of inverse functions.
- You have a new assignment
over section 2.7: implicit differentiation.
- You're invited! 2024
Math/Art Pop-Up Conference We'd love to have you
join us this Saturday, March 30, for
- Fun activities
- Free lunch! (Yes, there is!)
- Here's the link to sign up!
- Schedule:
- 9:00: Hyperbolic crochet
- 10:30: Origami
- 11:30: Lunch
- noon: Korean drumming
- Head's up: our third exam is Friday of next week.
- Please read Section 2.8:
Using Derivatives to Evaluate Limits for next time, and
carry out the preview. We'll wrap up this section before our
exam, but it won't be on the exam.
Then we'll be ready for Chapter 3: Applications of the Derivative
- Discussed the quiz, and some of the ins and outs of function composition, as well as the need to review the quotient rule.
- More about that derivative of \(\ln(x)\):
\[
\ln'(x)=\frac{1}{x}
\]
and that, more generally (since \(\frac{1}{x}\) is odd, and
must be the derivative of an even function), we "evenize"
\(\ln(x)\), and conclude that
\[
\ln'(|x|)=\frac{1}{x}
\]
that \(\ln(|x|)\) is the function whose derivative is \(\frac{1}{x}\) for all real numbers (except at 0, where none of these functions is defined).
- Then we moved on to the problem of translating from "calculus
inappropriate bases", and into base \(e\): e.g. when presented with
\(g(x)=2^x\), we translate that as \(2^x=(e^{\ln(2)})^x =
e^{\ln(2)*x}\) -- using one of the important properties of exponents.
This is a composition, but it's a simple composition of a linear function with the exponential function \(e^x\), and this is a more convenient form going forward (if we need to compute derivatives, etc.).
- Having made this translation, it is then easy to differentiate
\(g(x)=2^x\) using the chain rule:
\[
\frac{d}{dx}\left(a^x\right)=\ln(a) e^{\ln(a)x}=\ln(a) a^x = \ln(a) g(x)
\]
(I hope that you will soon think that the chain rule makes your life easy!:).
- Then we moved on to the "arcsine", the inverse of sine -- first
noting that sine is not really invertible, so we have to restrict the
domain:
Just as before, but once again we have to restrict the domain: sine is not invertible. We have a choice, but it seems like the best place to think of sine as invertible is on the interval $[-\frac{\pi}{2},\frac{\pi}{2}]$, on which it is invertible, so we restrict it, and draw in its reflection: arcsine! \(\arcsin(x)\), or \(\sin^{-1}(x)\). - Its derivative is
\[
\frac{d}{dx}\left(\arcsin(x)\right)
= \frac{1}{\sqrt{1-x^2}}
\]
- At the end of the hour, I suggested that you have a look at two
other functions whose derivatives we need:
- $f(x)=\cos(x)$ -- use restricted domain $[0,\pi]$
- $f(x)=\tan(x)$ -- use restricted domain $(-\frac{\pi}{2},\frac{\pi}{2})$
- But let's begin by returning to those last two inverse function:
arctan and arccos.
We proceed just as before, but once again we have to restrict the domain: cosine and tangent are not invertible. We have a choice, but it seems like the best place to think of tangent as invertible is on the interval $[-\frac{\pi}{2},\frac{\pi}{2}]$:
Once we've drawn it, it's easy to draw in the inverse function: Notice that arctan is a nice S-shaped curve, which is frequently used in math modeling to transition gradually between two states over a period of time: 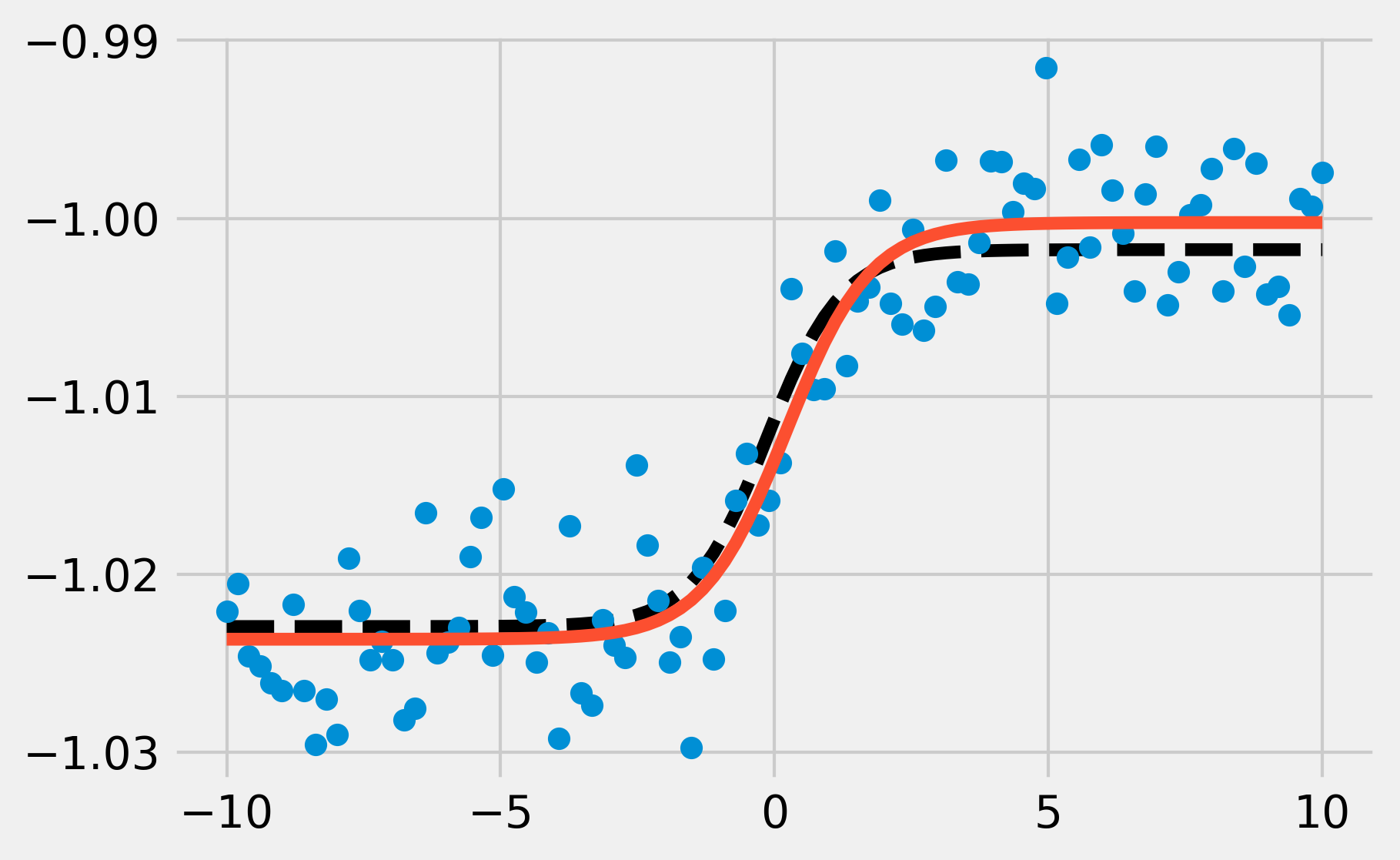
- Now how about its derivative? For $f(x)=\tan(x)$,
$f'(x)=\sec^2(x)$ -- still easy! But, as in the case of arcsine, it a
little more unpleasant to compute $f'(f^{-1}(x))$. We basically use the
same trick as before, however, with a twist: we can rewrite
\(\sec^2(x)\) in terms of tangent, using our favorite trig identity:
\[
\sin(x)^2+\cos(x)^2=1,
\]
Dividing by \(\cos^2(x)\) we get
\[
\tan^2(x)+1=\sec^2(x),
\]
Hence
\[
\frac{d}{dx}\left(\arctan(x)\right) = \frac{1}{\sec^2(\arctan(x))}
= \frac{1}{1+\tan^2(\arctan(x))}
= \frac{1}{1+(\tan(\arctan(x)))^2}
= \frac{1}{1+x^2}
\]
Because tangent and artangent undo each other. Thus
\[
\frac{d}{dx}\left(\arctan(x)\right)
= \frac{1}{1+x^2}
\]
(a rational function! Weird connections....).
- Now let's do it for arccos: we
have a choice, but it seems like the best place to think of
cosine as invertible is on the interval
$[0,\pi]$:
- Now how about its derivative?
You might recognize that it looks a lot like the arcsin function: in fact, we can see that it is the reflection of arcsin about the y-axis, followed by a shift up by \(\pi/2\): hence \[ \arccos(x)=\arcsin(-x)+\frac{\pi}{2}. \] That means we can get its derivative by the chain rule: \[ \frac{d}{dx}\left(\arccos(x)\right) = \frac{-1}{\sqrt{1-x^2}} \] - Today's new topic is Section
2.7: Implicit Differentiation -- I hope that you've had a
chance to read that, and to do the preview.
We'll approach this topic via some examples, such as the ones given in the section intro, and in the section preview. Let's start with the preview, as a sort of warm-up.
- Consider the relationship between x and y given by
$y = \frac{1}{x}$ We know how to differentiate y with respect to x, using the power rule: \[ \frac{d}{dx}y = \left(x^{-1}\right)' = -x^{-2} = \frac{-1}{x^2} \]
But there's another way to think about this relationship, and that's
$x y =1$ This gives no priority to either variable -- it's symmetric in both.
(This means that the graph of $y$ is symmetric about the line $x=y$ -- and that we could find the derivative of $y$ with respect to \(x\) from the derivative of $x$ with respect to \(y\)!)
We can still differentiate to find y'(x), however, using the product rule and something called "implicit differentiation". We consider $y$ and unknown (implicitly defined) function of $x$, treating it as $y(x)$; then, since both sides of the equation
$x y(x) =1$ are equal, the derivatives of both sides must be equal (we made the same argument when we used the chain rule to find the derivative of inverse functions!).
We differentiate both sides, and equate them (using the product rule on the left). From this we obtain the correct derivative, as well: \[ \frac{d}{dx}\left(xy\right) = y(x) + xy'(x) = 0 \] and solving for \(y'(x)\), we get \[ y'(x) = \frac{-y(x)}{x} = \frac{-1}{x^2} \]
- Probably the most important example for us to think about is a
circle:
Graph of $x^2 + y^2 = 16\text{.}$One of the issues is that this is not the graph of a function -- it fails the vertical line test. But it is clearly a really important graph for us to be able to do calculus on (e.g. make tangent lines).
One approach to dealing with this object is to divide it into two separate functions: an upper and a lower function, which would look like this: \[ y=\pm \sqrt{16-x^2} \] The upper function corresponds to the "+" sign, whereas the lower corresponds to the "-" sign. But what a pain! This is where dealing with it as an implicit function helps us.
The figure illustrates an example of a problem one might want to solve for the graph above: what is the slope of the tangent to the circle that goes through the point $(a,b)$?
I can think of two ways to solve this:
- Using geometry and symmetry (and just one equation); or
- Using two equations: the equation of the circle, and the equation of the tangent line.
The geometric solution shown in the figure is to use the slope \(m_r\) of the line between the origin and the point \((a,b)\), and to observe that the tangent line is perpendicular -- and hence has as its slope the negative multiplicative reciprocal, \(m_t=\frac{-1}{m_r}\).
But let's do it implicitly, by "differentiating the equation of the circle": \[ x^2 + y^2 = 16\text{.} \]
- Another example is the folium of Descartes, which is the graph
(solution) of the implicit equation
\[
x^3 + y^3 = 6xy
\]
Here the equation is perfectly symmetric in $x$ and $y$: it's not at all clear
which variable is dependent, and which independent. By the way, this
symmetry in $x$ and $y$ means that the graph of the solutions of the
equation must be symmetric about the line $\displaystyle y=x$:
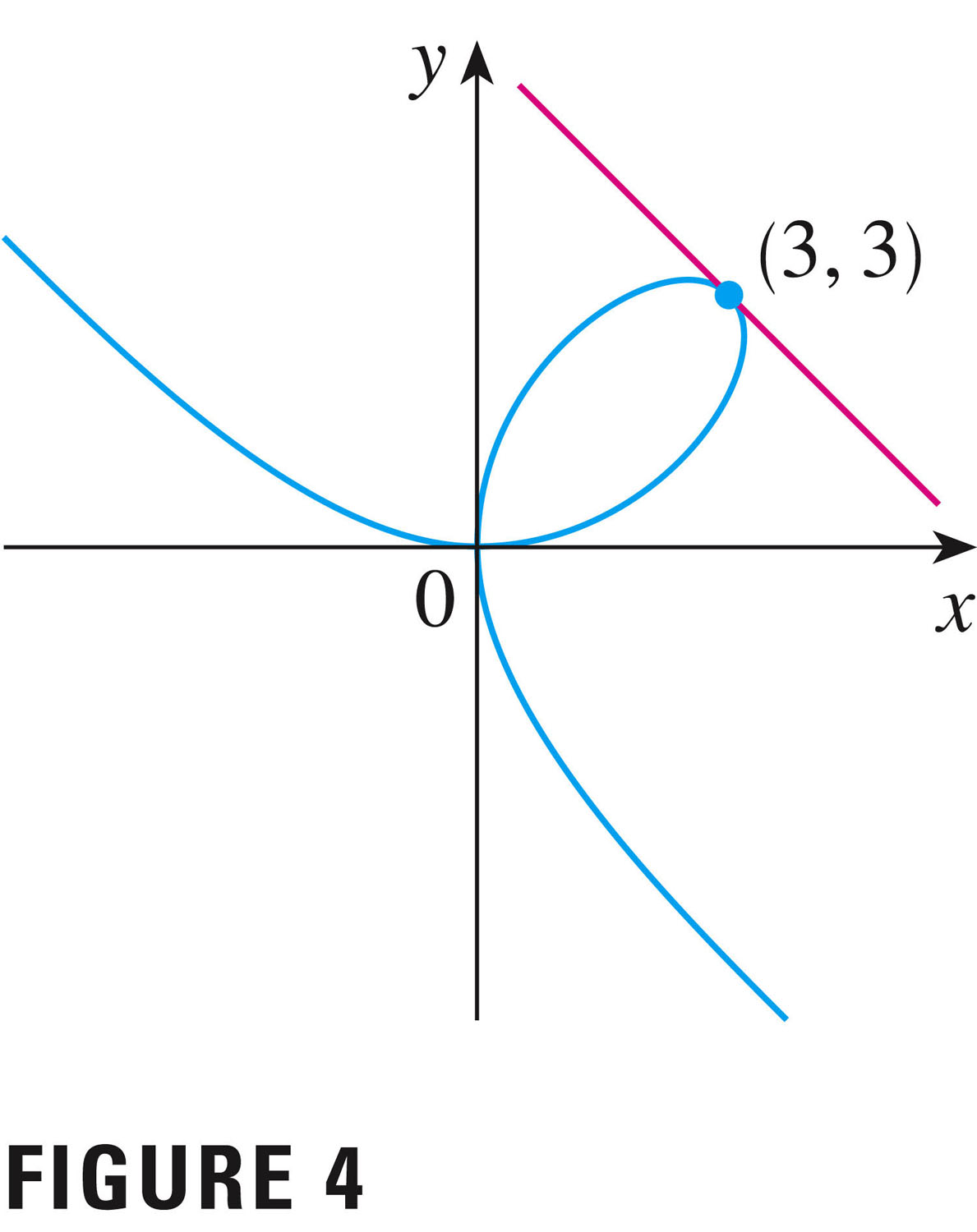
But you can see that this fails the vertical line test -- we can't call it the graph of a function.
Q: What is the equation of the tangent line shown? (Actually we can use symmetry alone to answer this question! That's a powerful notion....)
Even though the graph is not the graph of a function (either $y(x)$ or $x(y)$), we can still find tangent lines, etc., using ordinary derivatives. It is the case, however, that a single point in the plane can be represented by several different tangent lines (e.g. the point (0,0))
Q: What are the two equations of the tangent line to the point (0,0)?
- Here's a more complicated relationship between x and y given by
$x^2+y^2=(2x^2+2y^2-x)^2$ 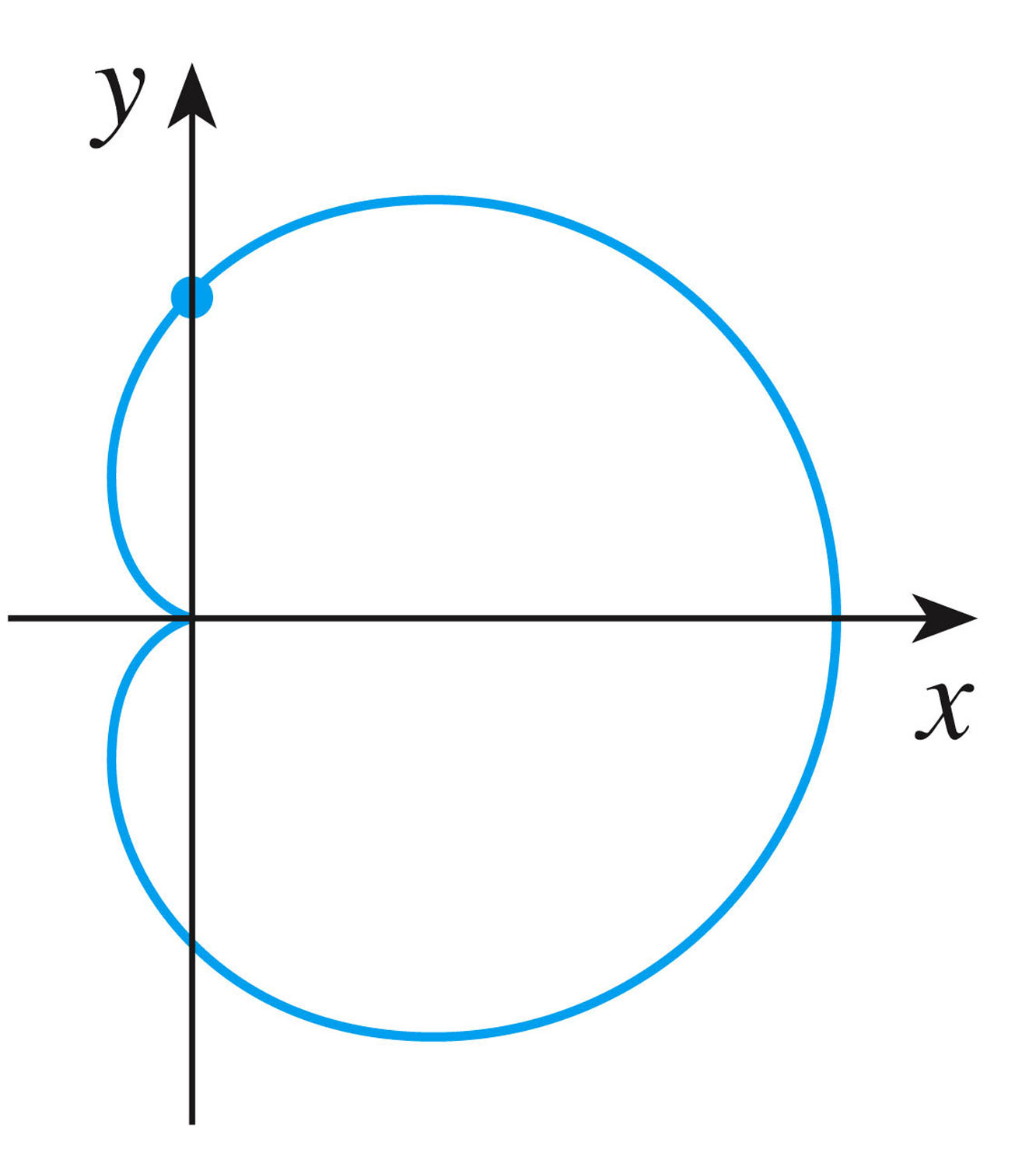
Because the equation is symmetric in $y$ (it's even in $y$), we expect the curve to be a reflection about the $x$-axis (as we can see in the figure).
So if $(x,y)$ is a point on the graph, then $(x,-y)$ will also be on the graph (and vice versa).
$x^2+y^2=x^2+(-y)^2=(2x^2+2(-y)^2-x)^2=(2x^2+2y^2-x)^2$ - Here's a worksheet for us to work on (it includes a few chain rule problems, too: from now on we'll be bumping into more compositions, and compositions shout "chain rule!").
- Consider the relationship between x and y given by
- A summary from another class: The Chain Rule
- Implicit differentiation summary
