- The quiz today will be over derivatives of inverse functions.
- Head's up: our third exam is Friday of next week.
You have an assignment over section 2.7: implicit differentiation. This is the last section covered on our upcoming exam, and we'll wrap that section up today with some examples.
- Sorry for the late posting of your 2.6 homework key.
We're starting to see some gnarly functions! Just take your time, and mind your stuff....
- Please read Section 2.8:
Using Derivatives to Evaluate Limits for next time, and
carry out the preview. We'll wrap up this section before our
exam, but it won't be on the exam.
Then we'll be ready for Chapter 3: Applications of the Derivative
- We started by reviewing the means by which we found the derivative for arcsine, and checked that it made sense.
- Then we went over the tricks by which we obtain the derivatives of
other inverse-trig functions whose derivatives we need:
- $f(x)=\cos(x)$ -- using restricted domain $[0,\pi]$
- $f(x)=\tan(x)$ -- using restricted domain $(-\frac{\pi}{2},\frac{\pi}{2})$
\[ \frac{d}{dx}\left(\arctan(x)\right) = \frac{1}{1+x^2} \] (a rational function! Weird connections....). \[ \frac{d}{dx}\left(\arccos(x)\right) = \frac{-1}{\sqrt{1-x^2}} \] - Then we started in on section
2.7: Derivatives of Functions Given Implicitly
In particular, we want slopes of curves which are not given explicitly as functions of \(x\) -- because they fail the VLT, in some cases, e.g. the circle:
Graph of $x^2 + y^2 = 16\text{.}$For a given value of \(x\) there are two values of \(y\) -- so we can't say "\(f(x)\)" and know which one we mean. (Mathematicians hate that!:)
Implicit differentiation provides a work-around.
- So let's see this work-around in action. Let's return to the
example of the folium of Descartes, which is the graph
(solution) of the implicit equation
\[
x^3 + y^3 = 6xy
\]
Here the equation is perfectly symmetric in $x$ and $y$: it's not at all clear
which variable is dependent, and which independent. By the way, this
symmetry in $x$ and $y$ means that the graph of the solutions of the
equation must be symmetric about the line $\displaystyle y=x$:
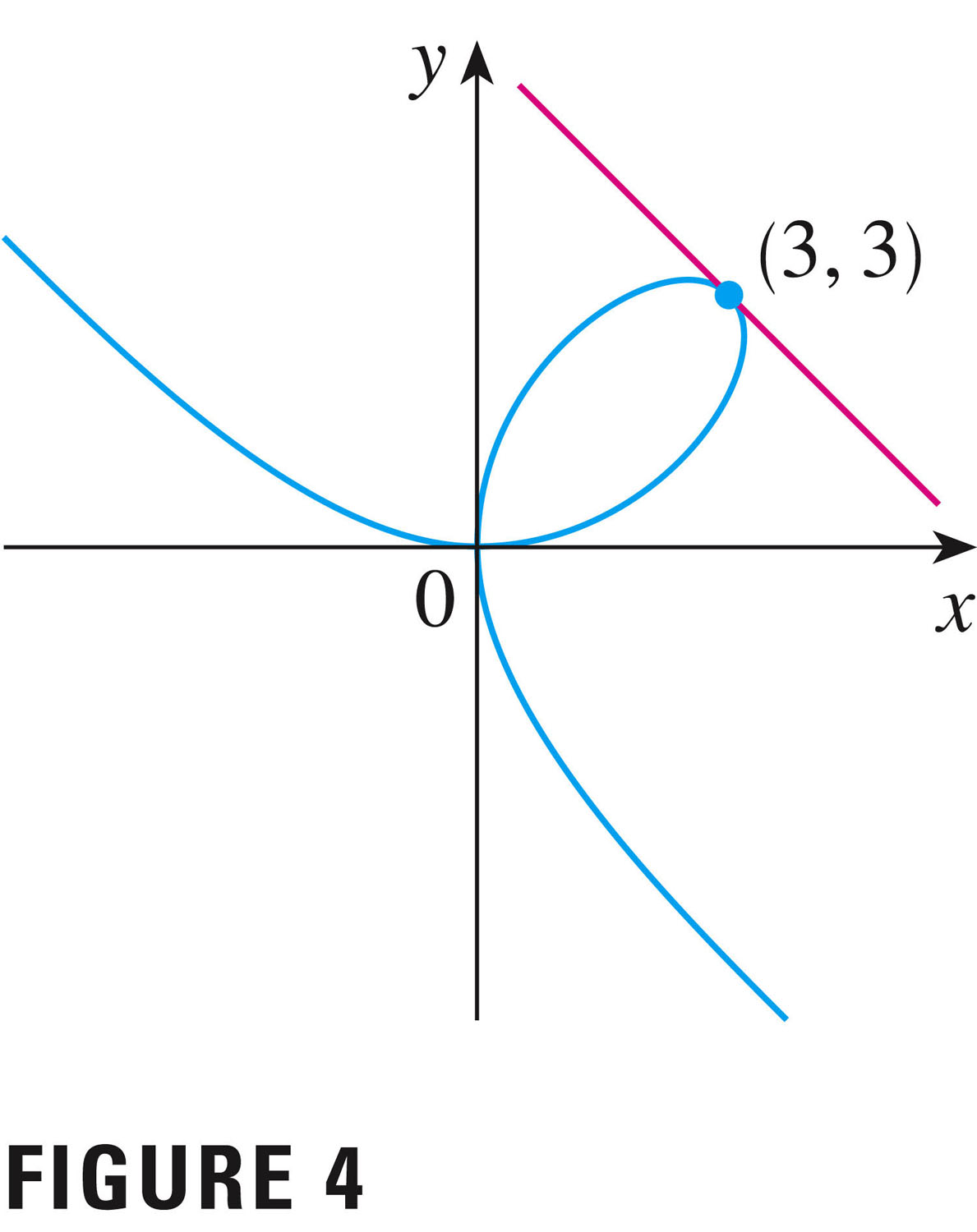
But you can see that this fails the vertical line test -- we can't call it the graph of a function.
Q: What is the equation of the tangent line shown? (Actually we can use symmetry alone to answer this question! That's a powerful notion: it has to be perpendicular to the line \(y=x\), since everything is reflected in that "mirror".)
\[ y-3=-1(x-3) \]
Even though the graph is not the graph of a function (either $y(x)$ or $x(y)$), we can still find tangent lines, etc., using ordinary derivatives. It is the case, however, that a single point in the plane can be represented by several different tangent lines (e.g. the point (0,0))
Q: What are the two equations of the tangent line to the point (0,0)?
- Here's a more complicated relationship between x and y given by
$x^2+y^2=(2x^2+2y^2-x)^2$ 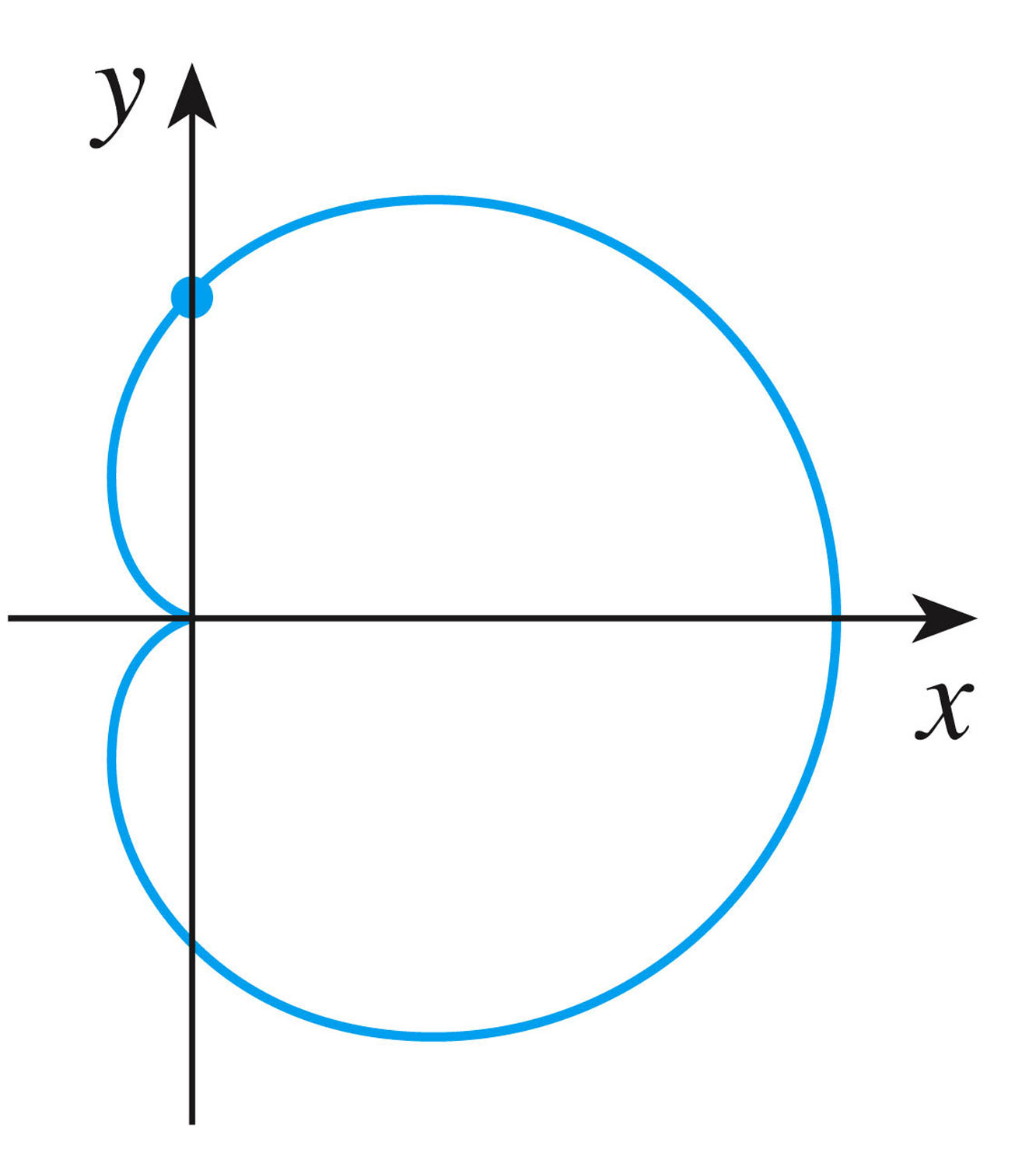
Because the equation is symmetric in $y$ (it's even in $y$), we expect the curve to be a reflection about the $x$-axis (as we can see in the figure).
So if $(x,y)$ is a point on the graph, then $(x,-y)$ will also be on the graph (and vice versa).
$x^2+y^2=x^2+(-y)^2=(2x^2+2(-y)^2-x)^2=(2x^2+2y^2-x)^2$ - Let's take a look at the worksheet that I gave you last time, and
we'll do a few problems to get ready for our quiz.
- 2a
- 4b
- Quiz
