- Today we'll continue with numerical integration: I hope that you've had a chance to read Vol
2, Sec 3.6: Numerical Integration.
- Per the lab exams:
- I've emailed back the Mathematica file that I worked
with. It has some detailed comments in it (if necessary).
I also calculated your grade for the first exam:
If it helps it's 1/3 of the total exam grade; if it hurts, it's 1/10 of the grade.
- "Divide Cell" is a command some of us need, so that you can execute just a little snippet of code. That way, if there's a fatal error, it doesn't stop further progress. We'll talk about it Friday.
- I'm sure that copy and paste is your friend in
this situation; being familiar with the
commands in your previous labs might have
handled most situations. Why not start a file
called "how to do various tasks"?
- I had to grade a little creatively, because it seemed unfair to punish too much for failure to plot something which wasn't defined....
- "Local linearization" was not well-understood:
Local because it's the tangent line function (i.e. linear), and represents the function very well at a point and in a (generally small) neighborhood around that point.
- For extrema and inflection points, you can see from the plot
that there are local max and min, and three inflection
points.
- Some of you struggled with the antiderivative. The
"easy" solution is to use Mathematica's Integrate
command, and then take the output and jam it into a new
function.
- The details (Wyatt wrote the key, nicer than mine!):
- I've emailed back the Mathematica file that I worked
with. It has some detailed comments in it (if necessary).
- Your quiz this week will feature a review of integration techniques (but not
numerical methods): trig integrals, trig substitution, and integration
by parts.
- There are times when we cannot find an explicit anti-derivative function
for an integrand, and hence we are obliged to resort to numerical methods:
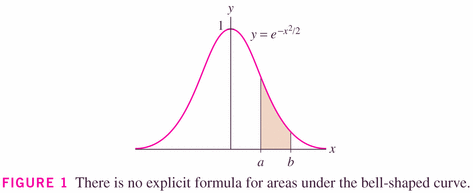
- There are various schemes for numerical integration (and it turns
out that each one of these relies on breaking that smooth area above
into rectangles, which seems pretty basic -- but maybe that's a good thing!):
- Left-endpoint Rectangle Rule.
- Right-endpoint Rectangle Rule.
- Midpoint Rule.
- Trapezoidal Rule.
- Simpson's Rule.
- Three of the rules are so called "rectangle rules" (LRR, RRR, Midpoint Rule);
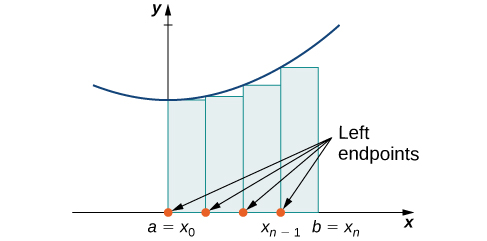
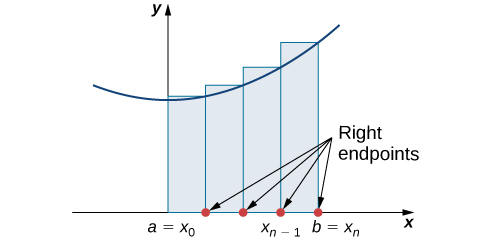
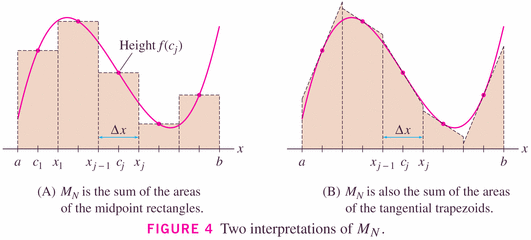
but as the image to the right (above) and the graphical insight below show, we can think of the Midpoint rule as being a "Tangent rule", another trapezoidal-type rule:
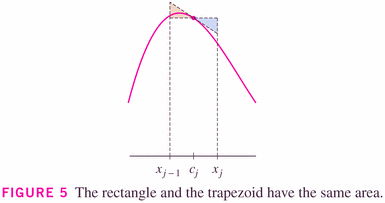
Midpoint Rule: \[ \int_a^b f(x) dx \approx M_n = \Delta x [f(\overline{x_1})+f(\overline{x_2})+\cdots+f(\overline{x_n})] \] where \[ \Delta x = \frac{b-a}{n} \] and $\overline{x_i}=\frac{1}{2}(x_{i-1}+x_i)=$ midpoint of $[x_{i-1},x_i]$.
- The Trapezoidal rule is really just the average of the Left- and
Right-rectangle Rules:
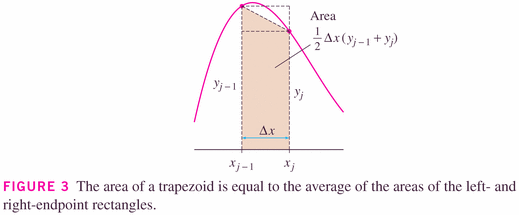
This gives rise to an important observation, which I encourage you to remember:
When you have two estimates, you have a third. (their arithmetic average, in this case). Notice that the two methods (LRR and RRR) make errors in the opposite sense in this case (and generally): one method tends to overestimate (the left, in this case), while the other tends to underestimate (RRR here); the average cancels their errors, to produce a more accurate estimate (in general).
Trapezoidal Rule: \[ \int_a^b f(x) dx \approx T_n = \frac{\Delta x}{2} [f(a)+2f(x_1)+2f(x_2)+\cdots+2f(x_{n-1})+f(b)] \] where \[ \Delta x = \frac{b-a}{n} \] and $x_i=a + i \Delta x$. This is just the average of the RRR and LRR: \[ LRR = \Delta x [f(a)+f(x_1)+f(x_2)+\cdots+f(x_{n-1})] \] \[ RRR = \Delta x [f(x_1)+f(x_2)+\cdots+f(x_{n-1})+f(b)] \] (and note that each of those methods ignores one endpoint).
Be careful however not to confuse the midpoint and trapezoidal rule. Each is effectively a trapezoid method, but the midpoint method uses "tangent trapezoids", while the trapezoid method uses "endpoint trapezoids" (and it turns out that the tangent trapezoids give better results, generally).
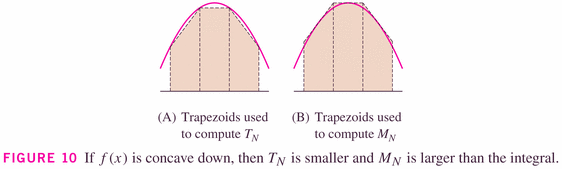
- Simpson's rule is a "blend" (or weighted average) of the Midpoint
and Trapezoidal rules, which perfectly balances the errors of the two
to generate a better rule:
\[
S_{2n}=\frac{2M_{n}+T_{n}}{3}
\]
Notice that the number of subintervals in Simpson's rule must be even.
Now we can go further (with Long's rule!:):
When you have two estimates, you have infinitely many more. (their weighted arithmetic averages).
- Let's start by considering a very simple example:
- Let's approximate the integral \[ \int_0^1 e^x d x \] using a step-size of 1.
- This is called a single "panel" -- we'll just use a single rectangle. Let's compare the results using our five methods.
- Here are the "error bounds" for the top three methods, showing
that the errors of midpoint and trapezoidal are related, and suggest
how to combine them to create a better method (Simpson's rule):


It turns out that the midpoint method is twice as good as the trapezoidal method, and the errors tend to be of opposite sign. This analysis is based off of an approximating parabola:
Notice that we're adding two copies of the Midpoint rule to one copy of the Trapezoidal rule -- so Simpson's rule has three estimates of the integral in the numerator (so we must divide that by 3 to produce a single estimate, Simpson's rule). Because the error of the Trapezoidal rule tends to be about twice the error of the Midpoint rule, and of opposite sign, the errors cancel in a beautiful way to create a cool new rule!
- Because of the forms of the error formulas, we can conclude something interesting:
- Trapezoidal and Midpoint rules get integrals of linear functions exactly right.
- Simpson's rule gets integrals of cubics exactly right! We leap over quadratics, straight to cubics. This seems almost magical....
- Let's reconsider our simple example:
\[
\int_0^1 e^x d x
\]
- Let's check the errors against the three methods' error bounds.
- We'll need some derivatives -- which ones?
- How do the actual errors compare to their bounds?
- Materials for today:
- Here's a nice summary of the topic, focused on the use of Mathematica to illustrate them. Interesting even if you don't use Mathematica.
- Numerical Integration on-line.
- Here is a hand out which emphasizes this message. Let's take a look at this:
- Mathematica code
- Check midpoint calculation
- Let's do the calculations by the formulas, for
- Trapezoid
- Simpson's
- Check that we get the same things using the averages
- Calculate the true value of the integral, and compare to the approximations. What's surprising?