- Our quiz Thursday will be over improper integrals.
- Since it won't break your hearts if we don't do a lab exam next
time, we'll do a regular lab instead.
- Our second exam is the Thursday following Spring Break. It will feature
- Numerical integration
- Improper integrals
- sequences and series
- Formally, a sequence is a function from the natural numbers ($\mathbb{N}$) into
the reals ($\mathbb{R}$), $a:\mathbb{N} \to \mathbb{R}$, given explicitly (by showing the terms), by
a formula, or by a graph. Informally, a sequence is a list of numbers
written in a definite order: e.g.
$\{a_1, a_2, a_3, \ldots, a_n,\ldots.\}$ The numbers $a_n$ are called
terms, and $a_n$ is called the $n^{th}$ term. Notice that it
appears that our sequence just keeps on going: often our sequences will
have terms corresponding to every natural number (the natural numbers
themselves form a sequence!), and so are infinite in extent (countably
infinite, like the natural numbers).
(By the way, do you know that there are different sized infinities? "Countably infinite" is the smallest. What's the largest?)
One famous sequence is the Fibonacci sequence, which is defined recursively by naming the first two terms in the sequence explicitly and then describing a pattern for the rest of the terms: \[ \begin{array}{l} {F_1=1}\cr {F_2=1}\cr {F_n = F_{n-1}+F_{n-2} \ \ n \ge 3} \end{array} \] This sequence appears throughout nature, and is named for the 13th century Italian mathematician Fibonacci Pisano.
- The sequence stems from a rabbit problem:
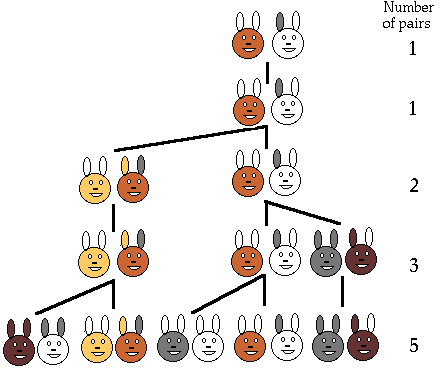
- Let's see where they came from, and why they're so special.
- They are the "worst case scenario" for the Euclidean algorithm to find the GCD (greatest common divisor) of two numbers, which we will investigate with this handout.
- The ratio of successive Fibonacci numbers approaches the golden mean as \(n \to \infty\): \[ \varphi = \frac{1+\sqrt{5}}{2} \approx 1.618 \]
- The sequence stems from a rabbit problem:
- We'll be interested especially in the behavior of sequences as the terms head
off to infinity. A sequence $\{a_n\}$ has limit $L$ and we write
\[
\lim_{n \to \infty} a_n=L \ \ \ \ {\textrm{or}} \ \ \ a_n \to L
\ \ {\textrm{as}} \ \ n \to \infty
\]
if for every $\epsilon > 0$ there is a corresponding integer $N$ such that
\[
|a_n - L| < \epsilon {\textrm{ whenever }} n > N
\]
If $\displaystyle \lim_{n \to \infty} a_n$ exists, then we say the
sequence converges, or is convergent. Otherwise we say
the sequence diverges, or is divergent.
In other words, a sequence is convergent to \(L\) if we can make the difference between the terms and the limit \(L\) as small as we like (\(\epsilon\)) by merely looking far enough down the road (from \(N\) on).
Hence when I say that "The ratio of successive Fibonacci numbers approaches the golden mean.", what I mean is that the sequence of ratios of successive Fibonacci numbers, \(a_n \equiv \frac{F_{n+1}}{F_n}\), converges to golden mean: \[ \lim_{n \to \infty} a_n=\varphi \]
-
Sometimes the sequence does not settle down to a limit, but diverges to
$\infty$: $\displaystyle \lim_{n \to \infty}a_n=\infty$ means that for
every positive number $M$ there is an integer $N$ such that
\[
a_n > M \ \ \ {\textrm{whenever}} \ \ \ n>N.
\]
Hence we can say that the sequence of Fibonacci numbers themselves diverges to infinity: their ratios converge, but the numbers are growing -- exponentially, actually, and a closed-form formula for them is given by \[ F_n = Round\left[\frac{\varphi^n}{\sqrt{5}}\right] \]
What I'm calling a "closed-form solution" (or formula) our authors would call the "an explicit formula for the \(n^{th}\) term of the sequence."
I really don't like problems of the form of Example 5.1 and Checkpoint 5.1! (The correct answer to those is "What do you want it to be?")
The 5.2 example and checkpoint are fine, because we've made clear what the pattern is. Using ellipses (...) is dangerous -- we don't know what happens next, for sure....
-
A sequence $\{a_n\}$ is called increasing if $a_n \le a_{n+1}$ for all
$n \ge 1$ (that is, $a_1 \le a_2 \le a_3 \le \ldots$. It is called decreasing
if $a_n \ge a_{n+1}$ for all $n \ge 1$ (that is, $a_1 \ge a_2 \ge a_3 \ge
\ldots$. It is called monotonic if it is either increasing or decreasing.
A sequence $\{a_n\}$ is called bounded above if there is a number $M$ such that \[ a_n \le M \ \ \ \ \ {\textrm{for all}} \ n \ge 1 \] It is called bounded below if there is a number $m$ such that \[ m \le a_n \ \ \ \ \ {\textrm{for all}} \ n \ge 1 \] If it is bounded both above and below, then it is a bounded sequence.
Hence the sequence of ratios of Fibonacci numbers, \(\{\frac{F_{n+1}}{F_n}\}\), is bounded above (by 2), and bounded below (by 1). The sequence \(\{\frac{F_{n+1}}{F_n}\}\) is a bounded sequence.
It is not monotonic, however. The values bounce above and below the limit, which is \(\varphi\).
- Theorems
-
Theorem 5.1: If $\displaystyle \lim_{x \to \infty} f(x) = L$ and
$f(n)=a_n$ when $n$ is a natural number, then $\displaystyle \lim_{n
\to \infty} a_n = L$.
It turns out that the \(n^{th}\) Fibonacci number \(F_n\) is given exactly by \[ F_n=\frac{\varphi^n - (-\varphi)^{-n}}{\sqrt{5}} \] That's an explicit function of \(n\).
While this function isn't real-valued defined for some powers of \(x\), we can formally take a limit of \(\{\frac{F_{n+1}}{F_n}\}\), and we'll see that it approaches \(\varphi\): \[ \lim_{n \to \infty}\frac{F_{n+1}}{F_n} = \lim_{n \to \infty}\frac {\frac{\varphi^{n+1} - (-\varphi)^{-(n+1}}{\sqrt{5}}} {\frac{\varphi^n - (-\varphi)^{-n}}{\sqrt{5}}} \] We can eliminate the \({\sqrt{5}}\), and pull a factor of \(\varphi\) from the numerator: \[ \lim_{n \to \infty}\frac {\varphi^{n+1} - (-\varphi)^{-(n+1)}} {\varphi^n - (-\varphi)^{-n}} = \lim_{n \to \infty}\varphi \frac {\varphi^{n} - (-1)^{n+1}\varphi^{-(n+2)}} {\varphi^n - (-1)^n\varphi^{-n}} \] which, upon dividing top and bottom by \(\varphi^n\), becomes \[ \lim_{n \to \infty}\varphi \frac {1 - (-\varphi)^{-(2n+2)}} {1 - (-\varphi)^{-2n}} = \varphi \lim_{n \to \infty} \frac {1 - \frac{(-1)^{n+1}}{\varphi^{2(n+1)}}} {1 - \frac{(-1)^n}{(\varphi)^{2n}}} = \varphi \] We actually rely on the following theorem not explicitly mentioned in the text to finish that argument, which I hope you will accept intuitively!
- Theorem: If $\displaystyle \lim_{n \to \infty}|a_n| = 0$, then $\displaystyle \lim_{n \to \infty}a_n = 0$.
-
Theorem 5.2: If $\{a_n\}$ and $\{b_n\}$ are convergent sequences
and $c$ is a constant, then
\[
\begin{array}{l}
{\lim_{n \to \infty} c = c}\cr
{\lim_{n \to \infty} ca_n = c\lim_{n \to \infty} a_n}\cr
{\lim_{n \to \infty} (a_n + b_n) = \lim_{n \to \infty} a_n + \lim_{n \to \infty} b_n}\cr
{\lim_{n \to \infty} (a_n - b_n) = \lim_{n \to \infty} a_n - \lim_{n \to \infty} b_n}\cr
{\lim_{n \to \infty} (a_n b_n) = \lim_{n \to \infty} a_n \cdot \lim_{n \to \infty} b_n}\cr
{\lim_{n \to \infty} \frac{a_n}{b_n} = \frac{\lim_{n \to \infty} a_n}{\lim_{n \to
\infty} b_n} \ \ {\textrm{if}} \ \ \lim_{n \to \infty} b_n \ne 0}
\end{array}
\]
Theorem 5.3 (Continuous Functions Defined on Convergent Sequences): Consider a sequence $\{a_n\}$ and suppose there exists a real number \(L\) such that the sequence $\{a_n\}$ converges to \(L\). Suppose \(f\) is a continuous function at \(L\). Then there exists an integer \(N\) such that \(f\) is defined at all values \(a_n\) for \(n \ge N\), and the sequence $\{f(a_n)\}$ converges to \(f(L)\).
- Theorem 5.4 (Squeeze Theorem): If $a_n \le b_n \le c_n$
for $n \ge n_0$ and $\displaystyle \lim_{n \to \infty}a_n = \lim_{n
\to \infty}c_n = L$, then $\displaystyle \lim_{n \to \infty}b_n = L$.
The "$n \ge n_0$" part says that the squeeze has to be on eventually, but not necessarily from the outset. It's the tail of the sequence that's important for the convergence, not the head.
- Theorem 5.5 (Convergent Sequences Are Bounded): If a
sequence $\{a_n\}$ converges, then it is bounded.
Note, however, that a sequence can be bounded but not converge -- for example \(\{a_n=(-1)^n\}\).
- The sequence $\{r^n\}$ is convergent if $-1 < r \le 1$ and
divergent for all other values of $r$: in particular,
\[
\lim_{n \to \infty}r^n = \left \{
\begin{array}{lc}
{0}&{-1 < r < 1}\cr
{1}&{r=1}
\end{array}
\right .
\]
- Theorem 5.6 (Monotone Convergence Theorem): Every
(eventually) bounded, monotonic sequence is convergent.
The point of adding "eventually" is that it is only the tail of a sequence that matters for convergence: what happens for any finite bunch of terms at the beginning won't have any bearing on the convergence as \(n \to \infty\).
-
Theorem 5.1: If $\displaystyle \lim_{x \to \infty} f(x) = L$ and
$f(n)=a_n$ when $n$ is a natural number, then $\displaystyle \lim_{n
\to \infty} a_n = L$.
- Summary
Sequences are like the natural numbers (1, 2, 3, $\ldots$.): they have distinct ordered terms traipsing off into the far distance. We're interested in what happens as the terms traipse off. Do they approach a fixed value? Do they oscillate, bouncing back and forth? Do they get larger and larger, or smaller and smaller? Several interesting example are included, such as the Fibonacci numbers (which came about from a silly rabbit population story problem in Fibonacci's Liber Abaci).
In this section we encounter many definitions, and a few theorems which help us to understand when a sequence converges (its terms approach a fixed value), or diverges (doesn't converge!). This is an issue of fundamental importance as we push on to our major objective: representing a function using an infinite sequence of functions! We start with numbers, of course, because that's a simpler case.
So the analogy we're working from is that \(\varphi\) can be approximated arbitrarily well by a sequence of ratios of Fibonacci numbers \(\{\frac{F_{n+1}}{F_n}\}\) as \(n \to \infty\).
We'll soon be doing the same thing for functions, rather than \(\varphi\)....
- Here's our handout for the unit (and the Mathematica file).
Let's take a look at some of the questions with your partner.
- Now it's on to Vol 2, Sec 5.2: Infinite Series
- Series are analogous to improper integrals, where the domain of
the integration trots off to $\infty$. We're trying to add up an
infinitely large number of things, and hoping that it will give a
finite number.
Naturally, this sounded a little odd to folks for a long time. It may even sound odd to you, and that's okay!
Zeno was a sophist -- like a lawyer -- who would take any case, and argue any position. He wrote several "paradoxes" that explored infinity, motion, etc., and tried to wrap his head around some very difficult ideas.
In one of his paradoxes, he showed that motion was impossible: thank God it appears that he was wrong!
He argued this way: to get to a wall, you have to first go half way; but to go half way, you have to go half of a half, or a quarter of the way; and before you go a quarter, you have to go an eighth; and so on, ad infinitum. So you can never get started, he argued.
Who can argue with that?:)
- Zeno understood, however, that it would certainly take
you an infinite amount of time to get to that wall (if you
could, which is impossible of course). Because you'd have to
go half way to the wall, and then half of a half, then half of
a half of a half, etc. So it will require an infinite number
of actions, which must take an infinite amount of time. So
you're safe if someone tries to shoot an arrow at you:

He would have found it odd that we might write \[ \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} +\ldots + \frac{1}{2^n} + \ldots = 1 \ (\textrm{Ouch!}) \] and so assert that the arrow would, indeed, get there. So we want to investigate this idea of adding up an infinity of numbers and yet getting a finite sum....
- We'll turn to our handout for this section (and here's the Mathematica file)
- Series are analogous to improper integrals, where the domain of
the integration trots off to $\infty$. We're trying to add up an
infinitely large number of things, and hoping that it will give a
finite number.
- Wolfram Alpha
- Mathematica on-line is an option, if you are at a computer without Mathematica installed. I've tried it and it worked pretty well!