The Absolute Value function is strangely mysterious. It's really quite simple, but many people have difficulty with it. I think that the problem is in how it's defined frequently: $$\begin{equation*}|x| = \left\{\begin{array}{cc} {x} \amp {x\ge 0}\cr {-x} \amp {x \lt 0} \end{array}\right.\end{equation*}$$

It almost seems as though it can be negative -- which it can't, of course. But it almost seems like it....

Maybe it's better to define it as $$\begin{equation*}|x| = \sqrt{x^2}\end{equation*}$$ where we understand the positive square root. Clearly $|x|\ge 0$ when you see it defined this way:

xxxxxxxxxx

f(x) = abs(x)

plot(f(x), (x, -2, 2), color='green',thickness=3)

The best way to think of $|x-y|$ is as the distance between numbers $x$ and $y$.

The idea behind the triangle inequality is clearly illustrated in the following figure:

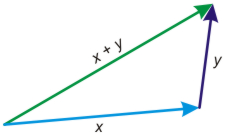
$$\begin{equation*}|x+y|\le|x|+|y|\end{equation*}$$

$$\begin{equation*}||x|-|y||\le|x+y|\end{equation*}$$

Put them together and what do you get? $$\begin{equation*}||x|-|y||\le|x+y|\le |x|+|y|\end{equation*}$$