Skip to main content
\( \newcommand{\lt}{ < } \newcommand{\gt}{ > } \newcommand{\amp}{ & } \)

Section5Calculus Background

There are many aspects of calculus that we need for numerical analysis. My contention is that we tend to motivate ideas in calculus with discrete approximations, then pass to the limit and replace all the discrete stuff with continuous versions.

We start with the idea of functions and their derivatives. Hopefully you're all feeling good about those:

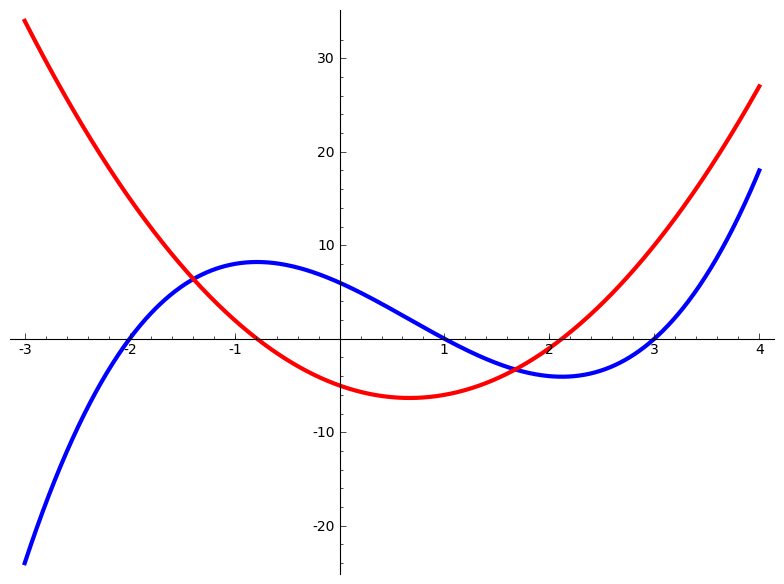
A function and its derivative
Figure5.1A third degree polynomial with a local max and a local min, along with its second degree derivative plotted on the same axes.
(especially in the case of polynomials).

Then, in numerical analysis, we go back and recall all those motivating examples and explain that, actually, that's how all this calculus stuff is computed....:)

Subsection5.1Taylor Series

The basic idea is to replace functions that are sufficiently nice (smooth, differentiable with enough higher derivatives) with polynomials, to give satisfying approximation.

The first case of interest is approximating a function by its tangent line at a particular point. The best linear approximator to a smooth (differentiable) function about the point \(x=a\) is \begin{equation*}f(x)\approx f(a)+(x-a)f'(a).\end{equation*}

The best quadratic approximating a function about the point \(x=a\) is \begin{equation*}f(x)\approx f(a)+(x-a)f'(a)+\frac{(x-a)}{2}f''(a).\end{equation*}

More generally,

Figure5.2Taylor series polynomial approximation
is the best \(n^{th}\) degree approximating polynomial.

What we're doing is matching the polynomial to the function and its derivatives at the point \(x=a\). The polynomials are doing a better job of capturing the behavior of the function \(f\) at that one point (and we hope that the polynomials are also doing a good job of capturing the behavior nearby, as well).

Here is sine, approximated with polynomials about the special point \(x=\frac{\pi}{2}\):

Figure5.3Using a zeroth degree polynomial (constant).
Figure5.4Using a 2nd degree polynomial (quadratic).
Figure5.5Using a sixth degree polynomial.

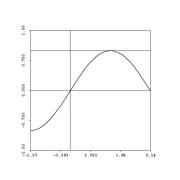
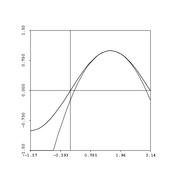
Watch Sage do this one:

Of course we're making an error:

Figure5.6Error in the \(n^{th}\) degree polynomial.

Let Sage show you the actual error on the interval \([0,\frac{\pi}{2}]\):

We do better on the interval \([0,\frac{\pi}{2}]\) (which is all we really need, if you recall) if we expand about \(\frac{\pi}{4}:\)