Day 4 in MAT229

Today:

• Announcements:
  • Calculus lab hours
  • Reminder to shut off and stash those cell phones and computers

• Questions about what we did yesterday, or homework?

• Reminder about poor notation:

  Many people will make the mistake of thinking that the inverse function is the same as

  The real problem is that we mathematicians are too lazy: we keep reusing notation, even to the confusion of our students.... We need to be attentive, and interpret the notation in context. Mathematicians are not alone, however: the same is found in language, right? What is "lead"? Did I lead a squad to victory, or were we mowed down in a shower of lead? If so, I led my squad astray....

  I almost commented yesterday on one of my pet-peeves of our language:

  it's -- "it is" (as in "it's quite a tail")
  its -- possessive form of "it" (as in "its tail")

  So ambiguity and confusion is not the exclusive problem of mathematics.

• Review of Section 6.2 (so far)
  • First of all, exponential functions have a characteristic shape:
    

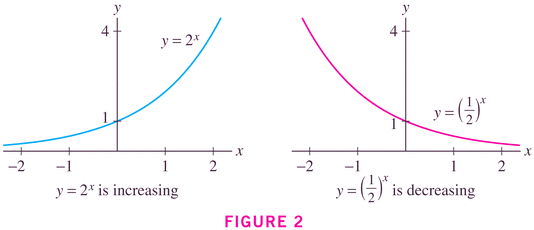
    This pair of graph should remind of us two important concepts that you will have heard about in science classes at some point: doubling time, and half-life.

  • Exponential functions are useful in all kinds of applications: whenever the rate of change of a function is proportional to the function itself, you'll see exponential functions putting in appearances.
    • Financial (bank accounts, loans, etc.)
    • Biology (population growth)
    • Forensics (Newton's Law of Cooling)

    This is written mathematically as

    

    The concept of "exponential growth" is often misused in common parlance, however: you'll often hear someone say that something's "growing exponentially!" -- by which they mean what? Growing really, really fast!!!! (many exclamation points....)

  • Shape as a function of base:

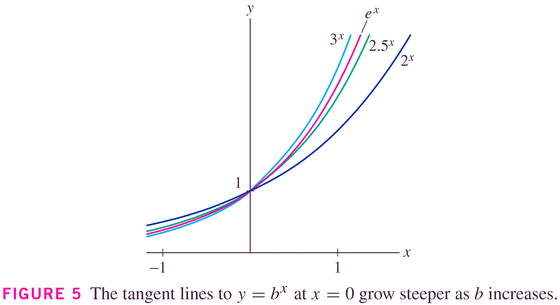
    There's one base that has a slope of 1 at (0,1): it's the special base e.

  • The following two properties are two sides of the same coin: but they're the most important reasons for the choice of the irrational base e:
    
    

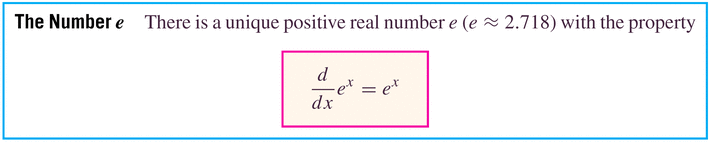
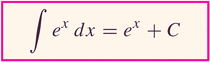
    This is almost a magical property: the rate of change of an exponential function is proportional to its value. In one case, the rate of change is the function value. The slope of the tangent line is the value of the function. Curious!

• Section 6.2: the exponential function (continued)
  1. Laws of Exponents:

  2. Demonstration of the derivative property of exponential functions (that an exponential function is its own derivative, up to a constant multiple).
     

  3. Do you think that this physical quantity (Total Global CO₂ emissions) shows signs of exponential growth?
     

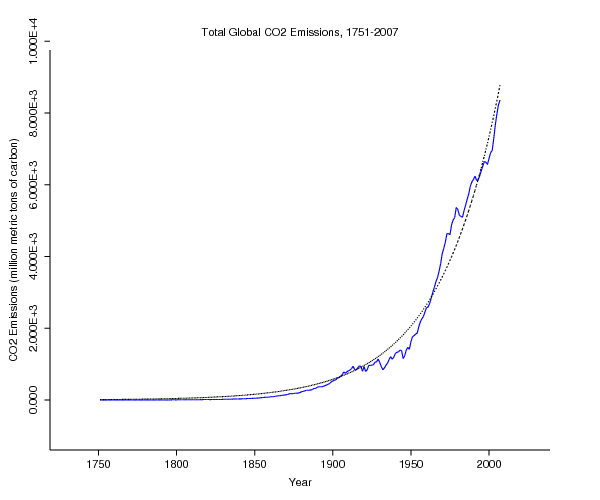
     The data is represented by the blue graph -- what do you suppose the dashed graph represents?

     Take a look at Figure 9, p. 395, in this section. Is the exponential doing a good job of fitting the data?

  4. Examples:
     1. #13, p. 401 (review of translations, reflections, etc., using )
     2. #17
     3. #36

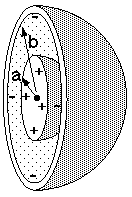
  5. Now I'd like to turn you loose on an exercise to compute the mass of the atmosphere:
     • Exponential Lab
     • This image might help for the actual calculation of the mass of the atmosphere:
       

     • Mathematica will compute the mass for us