Day 35 in MAT229

Today:

• Announcements:
  • Your next exam is this Thursday, and will cover the sections we studied from 7.2 to 11.1.
  • 11.1 Homework returned:

    When you randomly choose problems, this occasionally occurs: all the problems were "the same", which doesn't seem right. On the other, it allows me to recognize a really important issue. In this case, it's your apparent lack of willingness to use theorems and properties of functions.

    The property you need to use is this one:

    exponentials, trig, and rational functions are continuous on their domains.

    The theorem you need is this one:

    When taking the limits of compositions of continuous functions, one may pass the limit inside the composition.
    • 32 -- pass the limit inside the exponential function, which is continuous, and pass to the limit of the rational function.
    • 36 -- pass the limit inside the cosine function, which is continuous, and pass to the limit of the rational function.
    • 42 -- is a little trickier: you may see that as the difference of two (non-convergent) sequences, and hence say that it is non-convergent.

      But if you look at it from another perspective, this sequence is monotonically decreasing and bounded below -- hence it must be convergent.

      Say this:

      Bounded monotonic sequences converge.

• Section 11.2: Series
  • A series joke:

    An infinite number of mathematicians walk into a bar. The first one orders a beer. The second orders half a beer. The third order a quarter of a beer. The fourth orders an eighth, and so on.

    The bartender says "You're all idiots", and pours two beers.

  • Once we have some series in hand, we might want to start operating with them. In particular, as we saw in our very first series, we might want to add up the terms:
    

    We should get

    

    Such a sum is called an infinite series.

  • The question which presents itself is this: what do we mean by this sum of an infinite number of terms? This is indeed curious.

  • Here's how we make sense of that infinite sum:
    • From the sequence

      we define a new sequence :

      

      These are called partial sums. Notice that there are two indices running around, and that the limit refers to the summation's upper limit, not to the index of the sequence.

      If

      

      Then we say that

      

      exists, and is equal to . This justifies our probability distributions of the form

      

      Because, in general,

      

      This is an astonishing fact: we can think of an exponential function as a polynomial with an infinite number of terms. In fact, we can think of lots of functions this way (e.g. sines and cosines!). This is where we're headed in this class....

      More formally,

      

      Now geometric series are sufficiently important that it's useful to include that special case:

      

      There's a really fun proof of the first part above, based on a trick. Let's have a look at it, when :

      

      Multiply both sides by r, subtract, and solve for S.

      

      This theorem tells us that if a sequence isn't asymptotic to the x-axis, if the terms don't tend to 0, we can forget about its sequence of partial sums converging.

      Finally, series behave the way we'd hope:

      

    • Examples:
      • The harmonic series (Example 8, p. 732)
      • #1, p. 735
      • #2
      • #4
      • #15
      • #17
      • #61
      • #87
      • Beautiful spiral "proofs" of some infinite series

• Section 11.3: The Integral Test
  • concerns several different means of testing for convergence of series with all positive terms (obviously, if we're dealing with series of all negative terms, similar results are going to apply).

  • We're not so concerned with the actual limits (that is the values of the series) as we are with the convergence (or divergence) of the series.

  • Theorems:

    

    

    

    

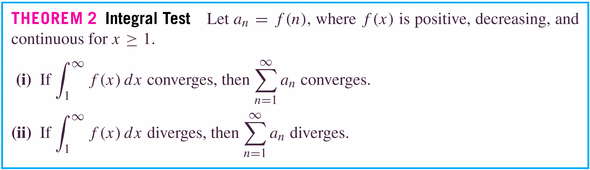
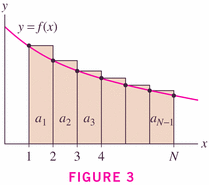
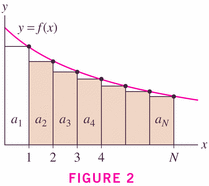
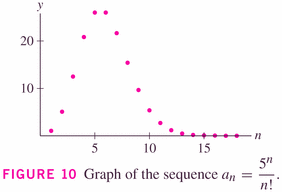
    Theorem 3 is just a corollary of Theorem 2, where the integrals are the obvious power functions:

    

    Let , where f is a positive, decreasing function. If converges by the integral test, and we define the remainder by , then

    

    (this gives us a bound on the error we're making in the calculation of a series). This is useful, for example, in the calculation of digits of (now, you might ask "and what's the use of that?!";).

  • Examples:
    • We can use this method to demonstrate conclusively that the harmonic series is non-convergent.
    • Dominoes (here's my page) -- and here's a more elegant page in Mathematica: Divergence of the harmonic series (and dominoes!)
    • #22
    • #36

• Section 11.4: Comparison Tests

  • Theorems:

    

    Notice how we can use each series to inform us about the other:
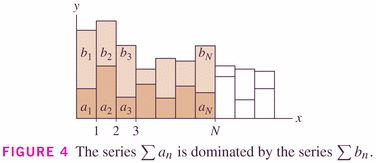
    1. if the series of the if finite, so is the smaller series of ;
    2. if the series of the if infinite, so is the larger series of .

    

    This comparison means that we'll need some series in our tool box with which to compare other series. The two obvious candidates are
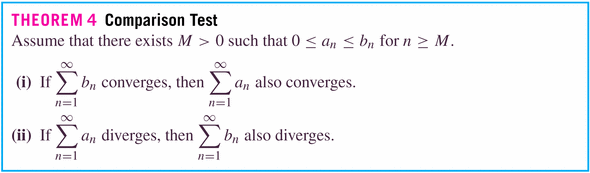
    1. geometric series, and
    2. p series, including
    3. the harmonic series (to show divergence).
    But once we have a known series, we can throw it into our toolbox, too!

    

    This theorem says that, in the long run, one series has terms which are simply a constant times the terms in the other series.

    In "the long run" means that we only really need to worry about the "tails" of series: we can throw away any finite number of terms for issues of convergence.

  • Examples:
    • #6, p. 750
    • #16
    • #28
    • #34 (draw a picture)
    • #46