Day 36 in MAT229

Today:

• Announcements:
  • Your next exam is tomorrow, and will cover the sections we studied from 7.2 to 11.1
    • 7.2 - trig integrals
    • 7.7 - approximate integration
    • 7.8 - improper integrals
    • 8.1 - arc length
    • 10.1 - parametric equations
    • 10.2 - calculus with parametric curves
    • 10.3 - polar coordinates
    • 10.4 - area and arc length of polar curves
    • 11.1 - sequences

• Section 11.3: The Integral Test
  • concerns several different means of testing for convergence of series with all positive terms (obviously, if we're dealing with series of all negative terms, similar results are going to apply).

  • We're not so concerned with the actual limits (that is the values of the series) as we are with the convergence (or divergence) of the series.

  • Theorems:

    

    

    

    

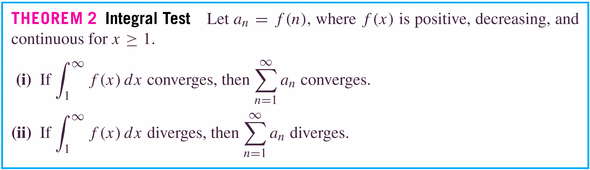
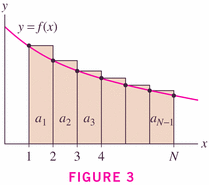
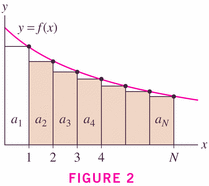
    Theorem 3 is just a corollary of Theorem 2, where the integrals are the obvious power functions:

    

    Let , where f is a positive, decreasing function. If converges by the integral test, and we define the remainder by , then

    

    (this gives us a bound on the error we're making in the calculation of a series). This is useful, for example, in the calculation of digits of (now, you might ask "and what's the use of that?!";).

    We can use this remainder inequality to get a bound on the true value of the series, just by adding to each part of the inequality:

    

  • Examples:
    • We can use this method to demonstrate conclusively that the harmonic series is non-convergent.
    • Dominoes (here's my page) -- and here's a more elegant page in Mathematica: Divergence of the harmonic series (and dominoes!)
    • #22
    • #36

• Section 11.4: Comparison Tests

  • Theorems:

    

    Notice how we can use each series to inform us about the other:
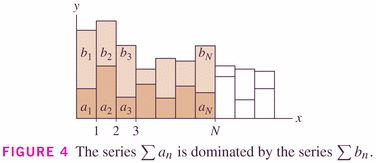
    1. if the series of the if finite, so is the smaller series of ;
    2. if the series of the if infinite, so is the larger series of .

    

    This comparison means that we'll need some series in our tool box with which to compare other series. The two obvious candidates are
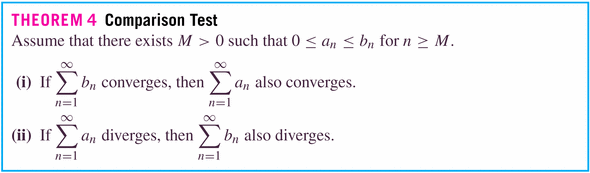
    1. geometric series, and
    2. p series, including
    3. the harmonic series (to show divergence).
    But once we have a known series, we can throw it into our toolbox, too!

    

    This theorem says that, in the long run, one series has terms which are simply a constant times the terms in the other series.

    In "the long run" means that we only really need to worry about the "tails" of series: we can throw away any finite number of terms for issues of convergence.

  • Examples:
    • #6, p. 750
    • #16
    • #28
    • #34 (draw a picture)
    • #46