Day 47 in MAT229

Last time

Next time

Today:

Announcements:
- Your 11.6 homework is due tomorrow
Section 11.8: Power series
- Summary:
  Now, rather than simply consider infinite sums of numbers, we're going to consider an infinite sum of functions in what are known as power series. They're like polynomials, but they don't have finite degree.
  The terms will be monomials -- functions with are simply constants times powers of x.
  Now we realize that, with functions for terms, each value of x specified gives rise to an infinite series, and we might immediately wonder if the series is convergent for a particular choice of ${x}$ .
  So what kind of function has an infinite number of terms? How do you evaluate such a thing? What kinds of function are these? It turns out that a lot of our old friends can be expressed this way
  ${F(x)={e^x}}$ , for example, as we've seen.
  Now what did we assert about ${F(x)={e^x}}$ ? That
  ${e^x=\sum_{n=0}^{\infty}{\frac{x^n}{n!}}}$
  For what values of x would this converge?
  
  Let's take a look at how well a truncated power series -- a partial sum -- approximates the real function.
  1. Graph ${e^x}$ on the interval [-2,2].
  2. Graph ${p_1(x)=\sum_{n=0}^{1}\frac{x^n}{n!}}$
  3. Graph ${p_2(x)=\sum_{n=0}^{2}\frac{x^n}{n!}}$
  4. Graph ${p_3(x)=\sum_{n=0}^{3}\frac{x^n}{n!}}$
  What do you see happening?
  
  Apply the ratio test for arbitrary x, and what do you discover?
  
  So ${F(x)={e^x}}$ presents us with a case where we have an "infinite radius of convergence".
  
  Interesting sidelight: you may have encountered Euler's Formula at some point in your life:
  
  ${e^{i\theta}=\cos(\theta)+i\sin(\theta)}$
  where ${i=\sqrt{-1}}$ . From this (and the power series for ${e^x}$ ) we can now deduce power series for the functions cosine and sine. Let's do that.
  Excuse me for saying, but this is very cool. It illustrates for you, as perhaps nothing ever has, the value of using imaginary (and complex) numbers.
  
  Let's look at an example where our radius of convergence is not so nice: consider ${F(x)=\frac{1}{1-x}}$ . One can show that
  
  ${\frac{1}{1-x}=\sum_{n=0}^{\infty}{\qquad{x^n}}}$ In fact we deduced this for a particular case when we looked at geometric series: that ${\frac{1}{1-r}=\sum_{n=0}^{\infty}{\qquad{r^n}}}$ But now we're talking about a function of x. One can think of x as representing allowable values of r (that is, values of r for which this geometric series converges). We know that this is for values of r such that .
  
  Now: for what values of x do you think that this will converge?
  
  Note that this is a variation on the theme of the ratio test: we don't consider the power terms, but only the coefficients.
- Examples:
  - What does Theorem 2 say will be the radius of convergence of the series for ${F(x)=\frac{1}{1-x}}$ ? What is its interval of convergence?
    Don't forget the endpoints!
  - How well do the truncated partial sum functions approximate ${F(x)=\frac{1}{1-x}}$ ?
  - #12, p. 769
  - #18
  - #19
  - #27
Section 11.9: Representations of Functions as Power Series
- Summary:
  Once we have one power series, we have an infinite number of other power series. We can use function composition to create others. [If you didn't have any respect for composition before, I hope you have some now!:)]
  So, for example, from ${F(x)=\frac{1}{1-x}}$ , we can produce series for
  1. ${\frac{1}{{1+x}}}$
  2. ${\frac{1}{1+x^2}}$
  3. ${\frac{1}{1-(x-3)^2}}$
  The other very important notion discussed here is the validity of differentiation and integration of power series. And the big news is that both operations are legitimate on the interval of convergence of the original power series:
  
  Hence, we can also generate the following power series from the series for ${F(x)=\frac{1}{1-x}}$ :
  1. What do you get when you integrate ${F(x)=\frac{1}{1-x}}$ ? How can we find a power series for this function?
  2. Given the power series for ${\frac{1}{1+x^2}}$ : what would be the power series of its anti-derivative(s)?
- Examples:
  - What do we get when we differentiate the series for ${e^x}$ term-by-term?
  - #5, p. 775
  - #9
  - #29
  - Let's take a look at a worksheet we are starting today.
Section 11.10: Taylor and MacLaurin Polynomials
- The big picture: we're approximating functions (some nasty) with nice ones (polynomials):
  
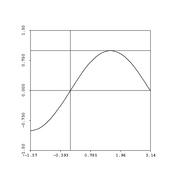
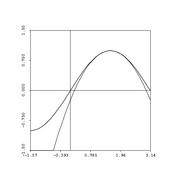
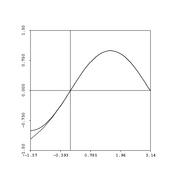
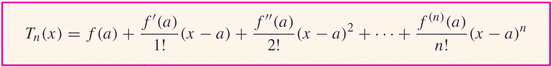
  Let's talk error now. Remember error? As we discussed for the case of Simpson's rule, it's nice to give an estimate -- but even nicer when you can provide an error estimate, also....
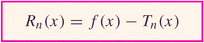
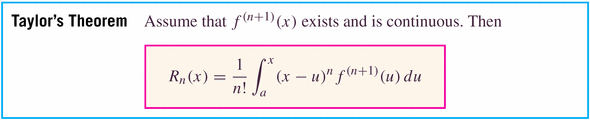
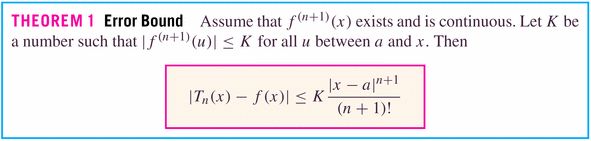
- Examples:
  - Taylor Polynomials Lab (from Stewart's Calculus)

Links:

Website maintained by Andy Long. Comments appreciated.
Updated on 09/30/2014 23:35:07