- There's a new assignment on the assignment page. Please keep an eye on
that page. If I change a deadline or an assignment for some reason,
I'll send an email.
- Let me begin by asking if there are any questions about our first
assignment, on section 1.2:
Once we've got questions out of the way, we're going to push on into sections 1.3 to 1.5.
Section 1.3: Algorithms
One might define algorithms as procedures for solving problems. The authors state that "The goal of numerical analysis [is] to construct algorithms for solving classes of problems...and to find general principles that are useful for constructing algorithms." (p. 12)
So the authors suggest two parts to the process:
- solving problems, and
- finding general principles.
Question: Is this really a good idea? How do you react to that?
The section concludes with an example algorithm, and oldie and a goodie (dating back to Babylonia, circa 2000 BCE): computation of a square root.
Let's try it out by hand, first: Let's attempt to find using this algorithm.
The really great thing is that I won't ask you to do this in base 60 (yet...:).
Our authors aren't quite as visual as I am, so I'm going to offer you what I think of as a helpful graphical display of the situation:
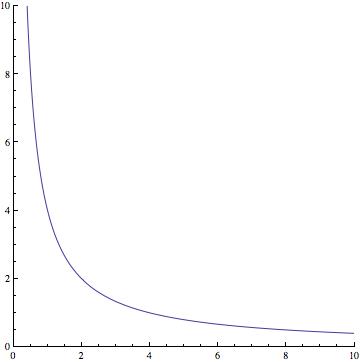
Question: Why do I present this particular graph? How does it help? What function is being graphed?
The code is actually contained in one-line of Computer problem #1, p. 15: (once the variable x is initialized, and the value of c is given):
The authors say that the "process can be repeated again and again; if it converges, then we can narrow down the search as close as we like."
The exercises on p. 14 move us toward the objective of demonstrating conclusively that the process converges. Let's take a look at #1 and #2.
Section 1.4: Error
Okay: we know that we're going to make errors. Even the Bible got wrong (
)!
But it won't always be so simple as a botched calculation of characteristics of a circle (1 Kings 7:23). There are other sorts of errors we're going to make through the the necessity of approximations:
- Approximating general functions with polynomials.
- All reals are rational, to a computer.
So, some important questions:
- How do we define errors?
- How do we measure errors?
- How do we avoid errors?
- How do we prepare for errors?
- How do we minimize errors (since we're guaranteed to get some)?
Our authors want to make sure that we are all on the same page with respect to errors, so we start with some definitions:
- Section 1.4.1: Definitions
-
error approximate value - true value
Our authors suggest that it is sometimes useful to have a name for the negative of the error:
-
remainder true value - approximate value
Or, to turn things around,
true value approximate value + remainder
However, "What we want is the error to be relatively small." (p. 15):
-
relative error And our authors then note that, combining these relationships, that we can write
approximate value = (true value)(1 + relative error) -
ulp: unit in the last place. The "unit in the last place" is what we think of as the error when we look at an approximation, such as this approximation of e (= 2.718281828459045....):
obtained by truncation (losing .000000008459045....)
I might have rounded, instead:
In either case, I believe in my heart that the error I'm making is less than .00000001 in size (which is a "unit in the last place").
Notice that, by specifying "in size", I'm ignoring sign.
As the authors say, "An error no greater than 0.5 ulp is always possible, but, as stated in Section 1.2, it is not always practical." In particular, we can get it down to a tenth of an ulp by moving to the next place value -- but that costs something.
-
decimal places of accuracy -
digits of accuracy Let's consider an example to discuss these two: Suppose that the true value is 1.2345, and that the approximate value found is 1.2346. Let's compute the decimals and digits of accuracy.
-
- Section 1.4.2: Sources of error
One of the things that the authors do in this section is discuss errors that we won't concern ourselves with: modeling errors, or programming errors, or hardware errors.
The errors they do care about they break into two types:
- Data errors:
- measurement errors, or
- errors passed to us by previous calculations.
- Computational errors:
- Roundoff Errors, or
- Truncation Errors
The authors make an amusing argument that just because we get error-riddled input doesn't mean that we can be sloppy. "It is best to treat the input values as exact and not make judgments about their accuracy or the morality of computing accurate answers to inaccurate problems." (my emphasis)
Data errors are propagated through further calculations (error propagation).
Let
be an approximation to datum
: then
propagated data error Then
computational error caused by inaccurately computing f. Figure 1.8 is a good one to illustrate these various sources of error, and the discussion.
- Data errors:
- Section 1.4.3: Specifying uncertain quantities
The authors consider a case where a quantity does not come to us as a value, but rather as a set of values. How do we proceed?
Obviously we could do a computation for each value. However then our audience is going to ask us for an answer, and we're going to have a bunch! They may not be okay with that....
We could use some statistics to give an answer. We could use the mean. But we want to avoid losing track (and failing to warn the user at the output end) that there was some variance in that input.
We treat the value as an interval (from lowest to highest data values), although we'd still have the problem of what to report.
This section provides a reality check on the term "significant digits" -- "there is no consensus on what this means" -- and they provide an example which illustrates the danger of going with the notion that the least significant digit should be in error by at most 5 units in that place. See Figure 1.9.
Can you assign a digit to the hundredths place that will not be in error by any more than five hundredths? The figure illustrates two cases which won't work -- 1.44 and 1.45 -- each producing an interval beyond what the data support (the top line).
If not, and we must use 1.4, then another user would assume that we only know the 4 in the tenths place to within five units, and you can see what happens to the actual uncertainty -- it expands grossly, to the interval (0.9,1.9).