- Your first homework set is due.
As a rule, please set that on the table, folded in half the long way, at the beginning of class.
- You have an assignment due next time, this Thursday, as well. Questions?
- There's a new assignment on the assignment page (it's due next Thursday).
Section 1.4: Error
Okay: we know that we're going to make errors. Even the Bible got wrong (
)!
But it won't always be so simple as a botched calculation of characteristics of a circle (1 Kings 7:23). There are other sorts of errors we're going to make through the the necessity of approximations:
- Approximating general functions with polynomials.
- All reals are rational, to a computer.
So, some important questions:
- How do we define errors?
- How do we measure errors?
- How do we avoid errors?
- How do we prepare for errors?
- How do we minimize errors (since we're guaranteed to get some)?
Our authors want to make sure that we are all on the same page with respect to errors, so we start with some definitions:
- Section 1.4.1: Definitions
-
approximate value - true value
Our authors suggest that it is sometimes useful to have a name for the negative of the error:
-
true value - approximate value
Or, to turn things around,
approximate value + remainder
However, "What we want is the error to be relatively small." (p. 15):
-
And our authors then note that, combining these relationships, that we can write
approximate value = (true value)(1 + relative error) -
ulp: unit in the last place. The "unit in the last place" is what we think of as the error when we look at an approximation, such as this approximation of e (= 2.718281828459045....):
obtained by truncation (losing .000000008459045....)
I might have rounded, instead:
In either case, I believe in my heart that the error I'm making is less than .00000001 (one "unit in the last place") in size. Notice that, by specifying "in size", I'm ignoring the sign of the number.
Question: put those two approximations and what I "believe in my heart" together, and what do you get?
As the authors say, "An error no greater than 0.5 ulp is always possible, but, as stated in Section 1.2, it is not always practical." In particular, we can get it down to a tenth of an ulp by moving to the next place value -- but that costs something.
-
-
Let's consider an example to discuss these two: Suppose that the true value is 1.2345, and that the approximate value found is 1.2346.
Using properties of logs, notice that
-
- Section 1.4.2: Sources of error
One of the things that the authors do in this section is discuss errors that we won't concern ourselves with: modeling errors, or programming errors, or hardware errors.
The errors they do care about they break into two types:
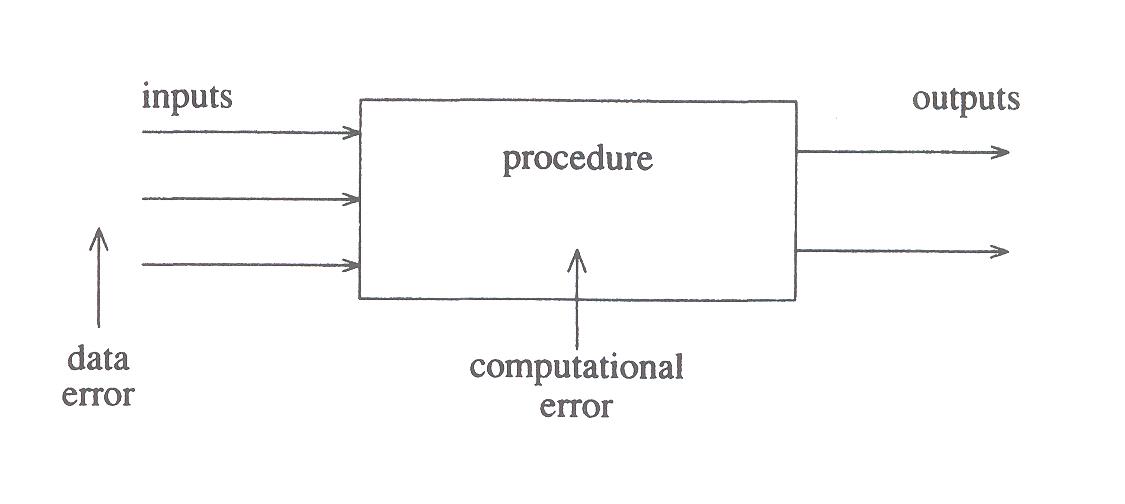
- Data errors:
- measurement errors, or
- errors passed to us by previous calculations.
- Computational errors:
- roundoff errors, or
- truncation errors.
We don't provide as many decimals as we've obtained, say, in a table. I guess we won't worry about those, either (but, in reality, you need to). It's related to that question "how many digits do I give my answer to?" that students ask.... We don't have a good simple answer.
The authors make an amusing argument that just because we get error-riddled input doesn't mean that we can be sloppy. "It is best to treat the input values as exact and not make judgments about their accuracy or the morality of computing accurate answers to inaccurate problems." (my emphasis)
Data errors are propagated through further calculations (error propagation).
Let
be an approximation to datum
: then
Then
caused by inaccurately computing f. Figure 1.8 is a good one to illustrate these various sources of error, and the discussion:

By the way, notice that if we add the errors we get
The total error is made up of the sum of the computational and data propagation errors.
- Data errors:
- Section 1.4.3: Specifying uncertain quantities
The authors consider a case where a quantity x does not come to us as a value, but rather as a set of values:
1.423, 1.399, 1.491, 1.449, 1.480 How do we proceed?
Obviously we could do a computation for each value. However then our audience is going to ask us for an answer, and we're going to have a bunch (a set)! They may not be okay with that....
We could use some statistics to give an answer. We could use the mean of the set of potential values. But we want to avoid losing track that there was some variance in that input (and failing to warn the user at the output end).
We could treat the value as an interval (from lowest to highest data values), although we'd still have the problem of what to report.
Let's assume that the true value lies within the data range: we assume that x lies in the interval [1.399,1.491]. So now the question is, what value might we assign to x?
This section provides a reality check on the term "significant digits" -- "there is no consensus on what this means" -- and they provide an example which illustrates the danger of going with the notion that the least significant digit should be in error by at most 5 units in that place.
See Figure 1.9:
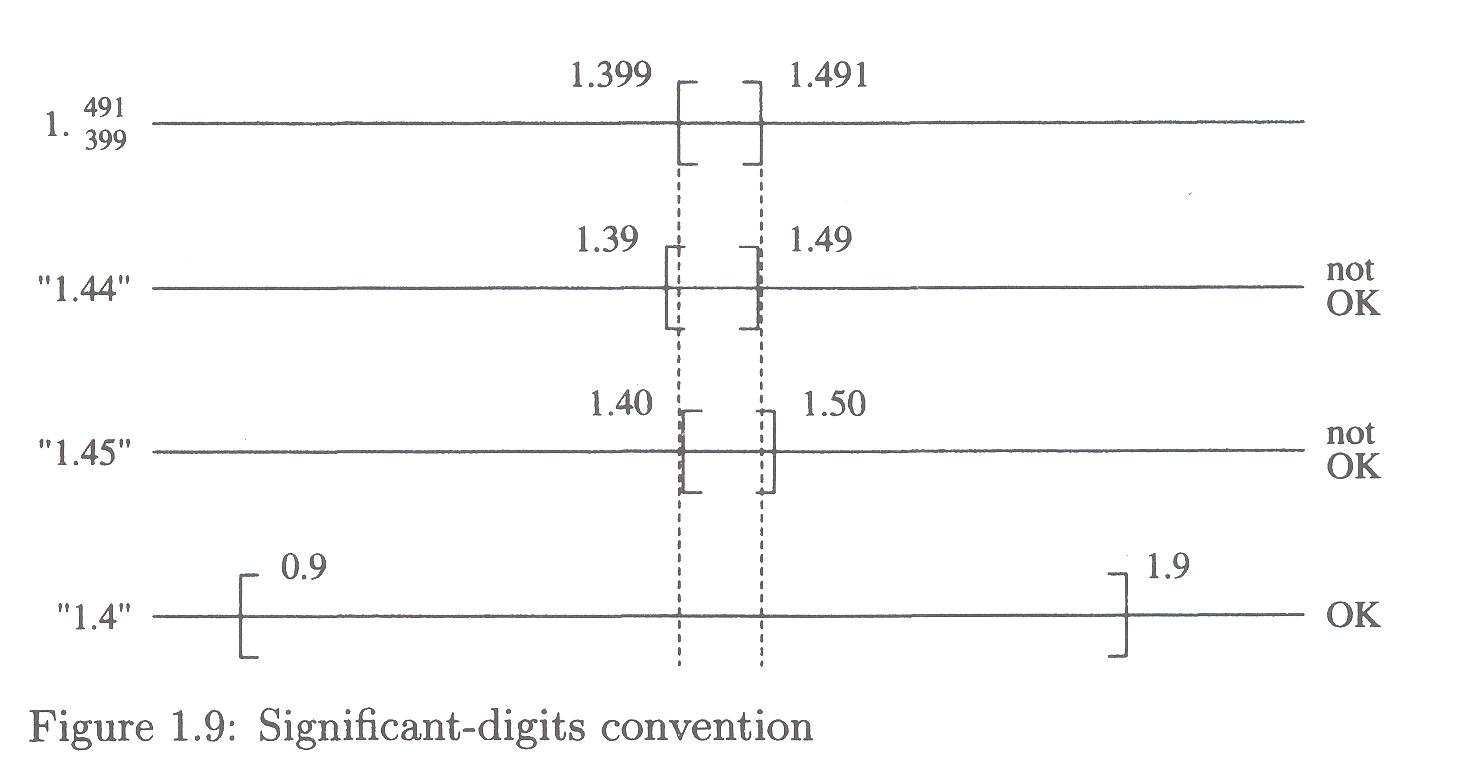
The question the authors ask (and answer) is this:
Section 1.5: Error Propagation
The authors give three examples of propagation of errors:
- Computation of a side of a triangle from two others.
- Roots of Wilkinson's polynomial
- Weather prediction (and chaos)
Ill-conditioned describes a problem that is sensitive to small changes in initial conditions; well-conditioned describes a problem that is insensitive to small changes in initial conditions.
- In the first example, a change of .1% in the length of a side leads to a 2.3% error in the calculation of the side of interest.
- In the second, a microscopic change in a single coefficient (-210 to -210+10-7) leads to 20% relative errors in the magnitude of some roots.
- In weather prediction, small changes in initial conditions can quickly lead to utterly different weather projections. (Authors claim 15 day limit in weather forecasting). There's nothing to do about this system, as it is chaotic.
We emphasize that, in this chapter, we are going to assume that the procedure itself is carried out exactly (e.g. square roots); the propagated error is simply a consequence of the procedure acting on error (not of how the procedure is implemented).
As examples, the authors consider the ordinary arithmetic operations (which are so-called "binary operations" (taking two inputs).
The first equation demonstrates the value of one of the equations we looked at last time: adding a and b, each with a little relative error, we get a sum which is in relative error by
or
so that
Imagine that there's no relative error in b. Then
and
Question: Under what conditions will this be much much greater (>>) than 1?
Let's take a look at an example where the errors cause trouble:
Interestingly enough, multiplication and division are robust ("well-conditioned") to data errors: performing a similar analysis (#3, p. 28), we have
or
so that
Again, imagine that there's no relative error in b. Then
Another way to simplify the analysis is to assume that the data errors are roughly the same size: then
- Section 1.5.1: Condition number of a unary operation
So now let's talk about some unary operations (e.g. cosine, rather than the binary operations we just considered). Again, we're going to assume that computations are carried out precisely -- it's just data error propagation we're concerned with at the moment.
The example our authors consider is one of a function
, given data
: then
Let's suppose that f is differentiable. If so, then we might make use of the Taylor Series Expansion. I told you earlier to expect it -- here it is, and it will occur over and over again.
If
and then
so that
or
which our authors call the relative derivative of
at
, and the condition number of
at
is the absolute value of the relative derivative of
at
.
In particular, this works better and better as
.
We can say, in particular, that the condition is directly proportional to the derivative, and to the size of a; it's inversely proportional to the size of
.
Examples: compute the relative derivative of
-
- Section 1.5.2: Interval analysis
I've got to say that I'm not a huge fan of interval analysis, in general. For example, in a problem exhibiting chaos, intervals can go haywire (source).
Interval analysis is well-behaved when the functions involved are monotonic (increasing or decreasing). But, as the authors illustrate, two different expressions for the same quantity can yield different intervals.
Think about the interval
for
. If you just check the endpoints, you get the single point 0.
And if a function is discontinuous, all hell can break loose!
Section 2.1:
"The main idea is that the computer works with a finite subset of the reals known as machine numbers." (p. 33)
- Section 2.1: Positional Number Systems
I might have started this chapter with Figure 2.3, on page 41:
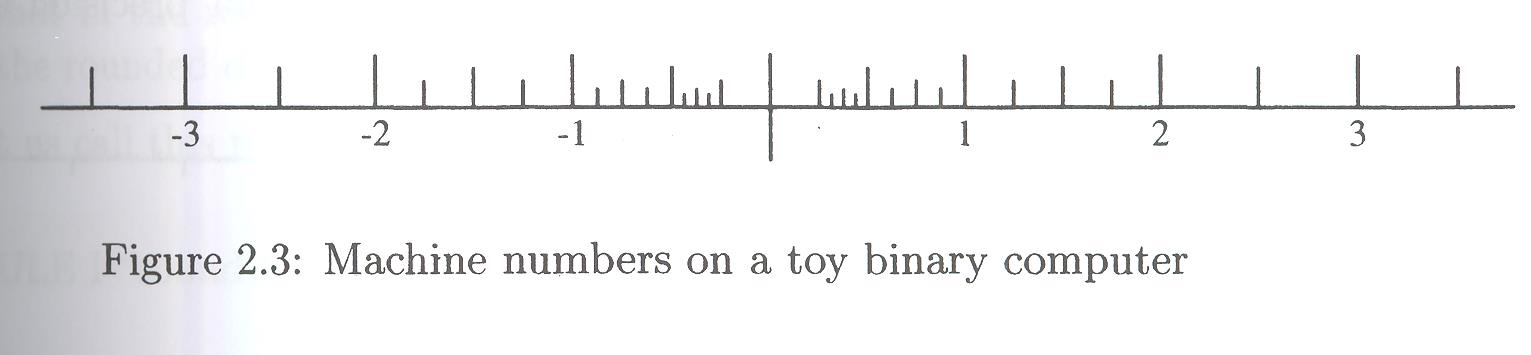
It gives a picture of machine numbers on a "toy binary computer". Section 2.1 makes a point about the need to consider other bases (other than 10). Among these other bases, the base 2 is probably the most important.
Question: why does base 2 figure so prominently in computer science?
There's a beautiful example here of how base 3 is used for tagging hogs:

Question: What other bases do you use? Why?
I've asked you to write a base converter for homework. Do you know how to convert from a one base to another?
- Suppose, for example, that you want to convert from 10 to 2; how do you do that?
- Then, how do you convert from 2 to 10?
Let's try a few. What's
-
in base 2?
-
in base 10?
- One more, with a twist:
in base 8?
- Section 2.2: Floating-Point Numbers
In this section the authors describe the manner in which machines are stored in the computer. They focus on "floating-point numbers", which are represented by three parts:
- The sign of the number
- The position of the "radix" point (aka decimal point in base 10)
- The mantissa (the known digits)
+2.99792458E08 (m/s) Question: What is that number?Definition 2.1: A real number is said to be an n-digit number if it can be expressed as
Question: They then ask "What's an n-bit number?" (p. 39) What do you tell them?
Let's imagine that our machine has base-10 architecture, with
, and
. Then we know exactly which numbers may be represented: numbers from
Largest magnitude numbers -9.999x109 +9.999x109 Smallest magnitude numbers -1.000x10-9 +1.000x10-9 ) is non-zero (except for 0 itself). This gives us exactly the same number of digits at each order of magnitude of 10.
If we allowed non-zero leading digits, then there would be redundant representations for many numbers (e.g. +1.000x10-9=+0.100x10-8)
Question: what do all the machine numbers look like if we restrict a machine so that it has architecture
, and
?
Now, in reality, computations are usually done in base 2, and the IEEE standard for single precision and double precision are
Single Double Base 2 2 n 24 53 e [-126:127] [-1022:1023] Question: in each case, how many exponents are there in the exponent range? Of what significance is that number?
Our authors describe the difference between precision and accuracy at this point: I think that it's best done graphically:

- Section 2.3: Rounding
"The purpose of rounding in computation is to turn any real number into a machine number, preferably the nearest one." (p. 43)
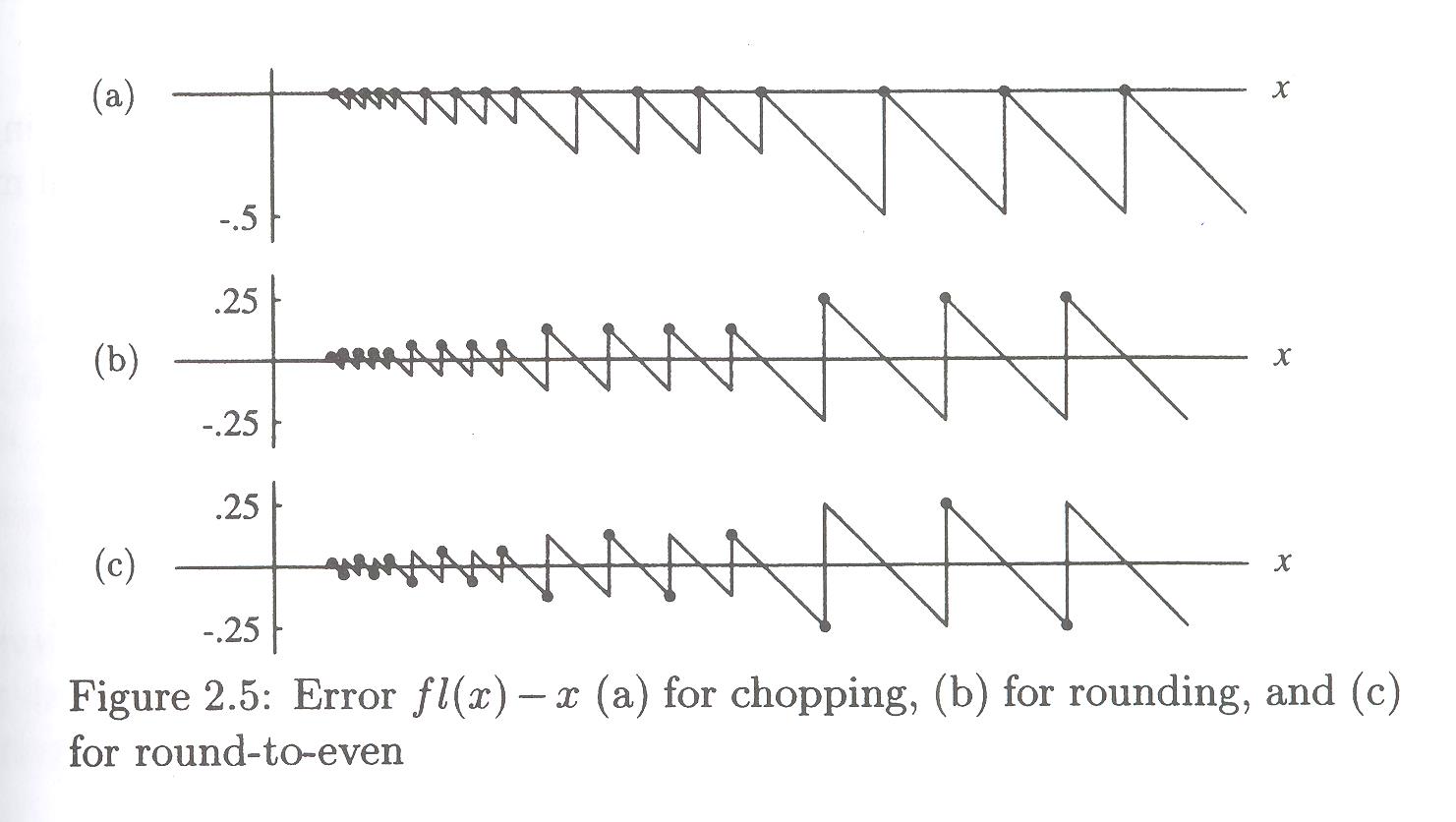
But there are different ways to do it. You're familiar with the "ordinary rounding" (but how do you handle ties -- that is, how do we round 19.5 to an integer?)). The authors suggest several strategies (p. 43)
- Rule 1: "round-to-even": if the digits following the nth digit are
- less than 500000....
then discard these digits - greater than 500000....
then discard these digits and add 1 to the nth digit - exactly equal to 500000....
then discard these digits and add 1 to the nth digit if it is odd.
"Round-to-even" because if nth digit is even, do nothing; add 1 if odd, making it even. All nth digits become even.
- less than 500000....
- Rule 2: "round-to-nearest, with round away from zero in case of a tie"
Same as Rule 1, except when exactly equal to 500000....
then round UP (away from zero).Inferior to Rule 1, as ever-so-slightly biased away from zero.
- Rule 3: chopping -- "round-to-zero" -- truncation.
Whatever comes after nth, just drop it.
Inferior to Rule 1, as slightly biased toward zero.
The biases are illustrated nicely in Figure 2.5, p. 45:
There is some vocabulary here with which we should be familiar: sometimes rounding results in- overflow (
)
- underflow (below the smallest possible machine number)
- NaN (not a number)
- Rule 1: "round-to-even": if the digits following the nth digit are