The Absolute Value function is strangely mysterious. It's really quite simple, but many people have difficulty with it. I think that the problem is in how it's defined frequently: \begin{equation*}|x| = \left\{\begin{array}{cc} {x} \amp {x\ge 0}\cr {-x} \amp {x \lt 0} \end{array}\right.\end{equation*}

It almost seems as though it can be negative -- which it can't, of course. But it almost seems like it....

Maybe it's better to define it as \begin{equation*}|x| = \sqrt{x^2}\end{equation*} where we understand the positive square root. Clearly \(|x|\ge 0\) when you see it defined this way:

The best way to think of \(|x-y|\) is as the distance between numbers \(x\) and \(y\).

The idea behind the triangle inequality is clearly illustrated in the following figure:

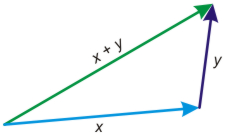
\begin{equation*}|x+y|\le|x|+|y|\end{equation*}

\begin{equation*}||x|-|y||\le|x+y|\end{equation*}

Put them together and what do you get? \begin{equation*}||x|-|y||\le|x+y|\le |x|+|y|\end{equation*}