The most important thing to realize about logarithms is that they are the inverse functions for exponentials:

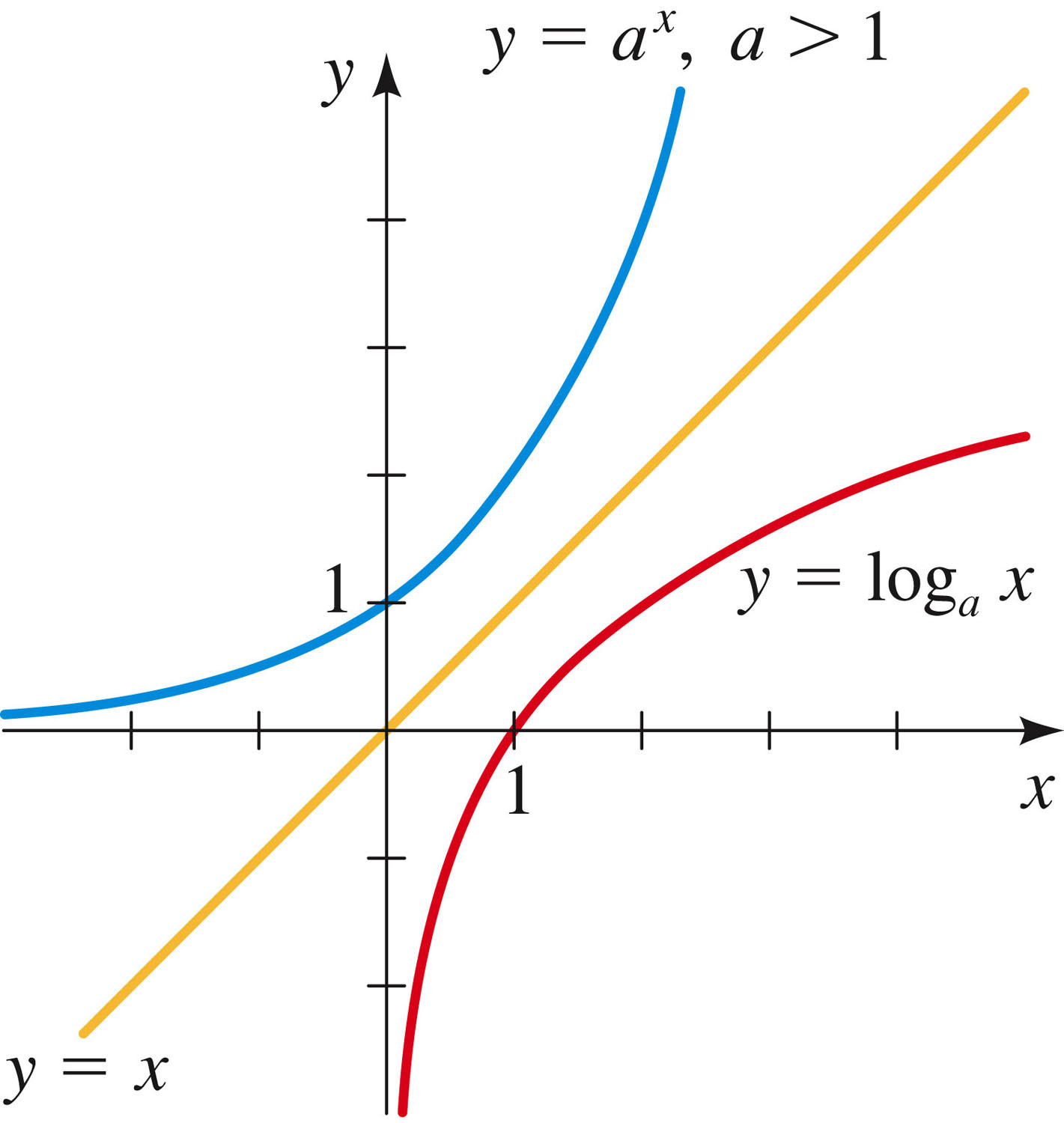
Then it's important to know that logs satisfy a variety of important properties:

Finally I should note one of the most useful tricks, which we use often in calculus to convert logs to natural logs. Suppose you have a log in base \(b\), and want to convert it to base \(e\): \begin{equation*}\log_b(x)=y \iff b^y=x\end{equation*} Hence, taking natural logs of the equivalent expression on the right, \begin{equation*}\ln(b^y)=\ln(x)\end{equation*} so that \begin{equation*}y\ln(b)=\ln(x).\end{equation*} But since \begin{equation*}y=\log_b(x),\end{equation*} we have \begin{equation*}\log_b(x)\ln(b)=\ln(x).\end{equation*} Finally, solving for \(\log_b(x)\), we have \begin{equation*}\log_b(x)=\frac{\ln(x)}{\ln(b)}\end{equation*} and we've successfully rewritten log base \(b\) in terms of the natural log, log base \(e\).

Of course we could use the same process to write log in any base in terms of any other base. We simply prefer base \(e\) in calculus because \(e^x\) has that magic property that it's its own derivative.