Math Modeling: Day 27

1. MINIMAX Workshop Summary

   G. Kukla, T. Karl, M. Riches

2. (p. 1): Maximum and minimum temperatures: A backward and a forward look

   D. E. Parker

3. (p. 13): The effect of artificial discontinuities on recent trends in minimum and maximum temperatures

   D. R. Easterling, T.C. Peterson

4. (p. 161): The climate record: Charleston, South Carolina 1738-1991

   DJ. Smith

5. (p. 231): Cloudiness trends this century from surface observations (Abstract)

   K. McGuffie, A. Henderson-Sellers

6. (p. 327): DTR and cloud cover in the Nordic Countries: Observed trends and estimates for the future

   E. Kaas, P. Frich

7. (p. 399): Predicted and Observed Long Night and Day Temperature Trends

   Patrick J. Michaels, Paul C. Knappenberger and David A. Gay

One student gets a C for emailing about it -- there was only one student who even emailed something.

I gave you this assignment as a bit of a test. The answer was on the 7th page of the document (so you had to wade through some boring stuff to get to it); but I found it by going straight to the decade of the 1890s, to see if something dramatic happened there -- and it did:

Temperature data taken previously through the years is not entirely comparable to those collected since the mid-1890s, but do form useful data for historical climatological study. [my emphasis]

But the fact that 0/14 students found what is staring one in the face, provided one reads it, suggests that no one read it. So how do I run with this information?

1. "If a tree falls in a forest and no one is around to hear it, does it make a sound?"
   
2. "If a tree falls in the forest, but nobody hears, did it fall?"
3. "Who cares about trees, anyway?"
4. "I got more important things to do right now...."

This one's due this Friday. If you have questions about that, please email me, and maybe we can get you straightened out. Some of you seem very reluctant to reach out -- please do!

1. I've prepared a "pre-print" of the paper that could result from our work on the Fletcher data. I'll share it with you on Friday. In particular, I want to incorporate any of your ideas from your "book reports" (of which I have a very sad grand total of 6/14).

2. I've done a little preliminary work on some models which we have not discussed. Here's the big picture: I'd like to be able to simulate weather over the 100 years (from 1893 to 1992, which we take as our data set based on Fletcher's remarks, above).

   We'll base those simulations on what the climate has looked like in Wood County in the past. So there are two data sets, and two graphics which I would like you to reproduce based on those data sets. These will help us to create a weather simulator which will resemble the weather of Wood County.

   I'm going to make it a little easier on you than I made it on me: I had to digitize some of the data. But I'll just give it to you!

   Your job: by Friday, reproduce these figures. I don't care what software you use, but we did this using Mathematica early on. Include your model fits. Present this as a report to me (i.e. perhaps two pages, typed).

   1. Problem 1: Fletcher gives us the record temperatures, as well as the years in which they occur. Let's focus on the temperatures for a moment. What if you try to fit a sine function to all of this extreme data -- the maxmax, minmax, maxmin, and minmin data -- simultaneously?

      We might hope that this would give us a good approximation to the mean across the span of a year.

      You might get something like this:

      

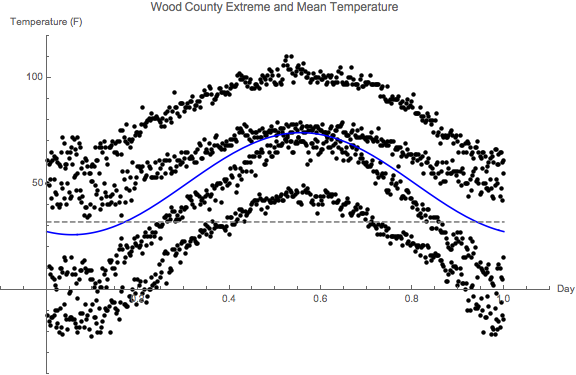
      Here's all the data: use regression -- linear or non-linear -- to find that function. Either will work!

      This is kind of an odd regression problem, because, as you can see, we don't do a very good job of fitting the data! But we're trying to construct an average of all of this data -- not fit any particular data point.

   2. Problem 2: Fletcher gives us (on pages you haven't seen) the climate variables Mean Temp, Mean(max), and Mean(min) for the 30-year period 1959-1988 (for the first two), and 1949-1978 for Mean(min).

      We can fit pretty nice sine functions to those three data sets too, and here they are:

      

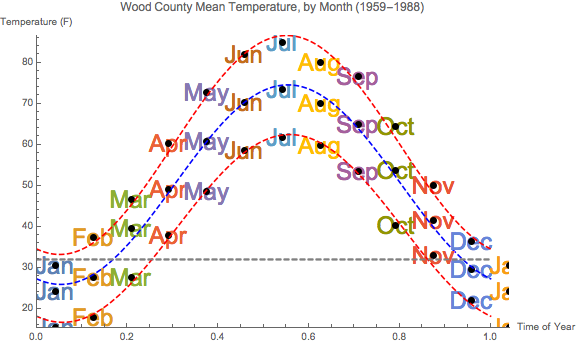
      Here's all the data: use regression to find those three function.

3. You don't have to reproduce this figure, but I wanted to show you what they all look like when plotted together, with Fletcher's record extreme data:
   

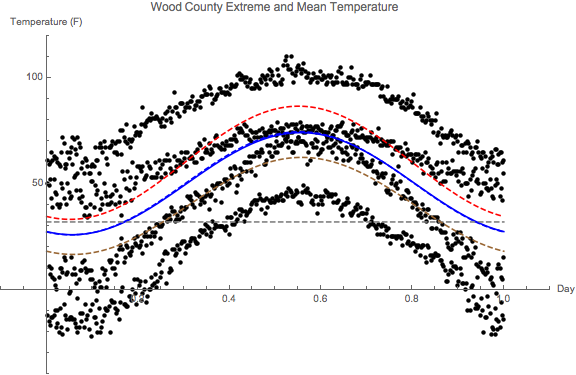
   The mean curves are the blue in the middle. The exceptional thing is that the two mean curves (in blue, one solid, one dashed) are almost exactly on top of each other -- but one was created using 1464=4*366 data points (all of Fletcher's extreme temperature from his tables), whereas the other was created from 12 pieces of data (the climate averages). The two red curves are the fits to the Mean(Max) and the Mean(Min) climate variables (again, 12 pieces of data each).

   In my mind I imagine the trajectory of weather getting off "the climate track" (which is represented by the blue -- mean -- and red -- max and min -- curves). Imagine a normal distribution of potential temperatures, whose mean is supposed to be along the blue track, but it wanders; and, as it does, its maximum may go way up there (as will its maxmin); or it could wander low, and its minimum will go way down there (as will its minmax).

   That's the story!

   So the next question is this: how is the weather wandering?

   We have the rest of the semester to figure that out....

Some good links that I might recommend (a few of which we'll focus on):

1. A great intro to many of the most important question: "When a new virus emerges, no one is immune. A highly transmissible virus, like the coronavirus behind the current pandemic, can spread like wildfire, quickly burning through the dry kindling of a totally naive population. But once enough people are immune, the virus runs into walls of immunity, and the pandemic peters out instead of raging ahead. Scientists call that the herd immunity threshold."

2. How epidemics like covid-19 end (and how to end them faster): A coronavirus causing a disease called covid-19 has infected more than 70,000 people since it was first reported in late 2019. To predict how big the epidemic could get, researchers are working to determine how contagious the virus is.

3. The SIR Model for Spread of Disease - Introduction (from the MAA).

   In particular, we will implement The SIR Model for Spread of Disease - The Differential Equation Model in InsightMaker.

4. Mathematics of the Corona outbreak, with Professor Tim Britton

   (An excellent introduction to SIR models, from both the infectious disease and mathematical sides)

   Questions:

   1. Where is the "calculus moment" in this video?

   2. How does Britton suggest breaking $R_0$ down into "actionable" pieces?

5. This Covid-19 situation is probably more suited to a SIRDs model (with disease-induced death).

6. An on-line model developed by Ashleigh Tuite and David Fisman, Dalla Lana School of Public Health, University of Toronto

7. This one incorporates space into the model. These models are called "agent-based models".

8. Could Coronavirus Cause as Many Deaths as Cancer in the U.S.? Putting Estimates in Context

   This on-line estimator (i.e., a model!) allows one to estimate deaths, as well as death by age-category.

9. A nice R-based introduction to infectious diseases and nonlinear differential equations.

10. Use of a log-scale (which they take pains to explain) to illustrate deaths by country, updated daily. There is even a separate page at the New York Times to explain log plots: "A Different Way to Chart the Spread of Coronavirus: Those skyrocketing curves tell an alarming story. But logarithmic graphs can help reveal when the pandemic begins to slow."